1．はじめに

流出モデルにはタンクモデル，貯留関数法，表面流モデルなど色々なものがありますが，本記事では貯留関数法という手法について紹介したいと思います．

大学で水文学を受講していた方にとって，貯留関数法という名前は何となく聞いたことがあるものだと思いますが，貯留関数法の考え方や実際の計算プロセスについて知っている学生・若手技術者の方はそんなに多くないと思います． 本記事では，そんな学生や若手技術者の方々を対象に，原理の説明から実際の計算過程に至るまで，できるだけ詳しく解説していきたいと思います．

前編は貯留関数法の成り立ちとその考え方，計算方法などについて紹介します． 後編では，計算アルゴリズムとプログラム，計算結果を記載しています．

なお，わかりやすさを優先しているため，厳密性を欠く部分もありますがご容赦ください．

普段プログラミングをしない人にとって，今回のプログラムは長く見えるかもしれませんが，ボタン1つで計算できるようになっているのでご安心ください． プログラムの動かし方については後編で解説します．

【流出解析】シリーズ　一覧

【流出解析】シリーズ　第1回　流域界の決定と入力データの用意 【流出解析】シリーズ　第2回　貯留関数法【前編】 【流出解析】シリーズ　第3回　貯留関数法【後編】 【流出解析】シリーズ　第4回　流域実蒸発散量の推定―蒸発散比法― 【流出解析】シリーズ　第5回　実蒸発散量の推定―補完法― 【流出解析】シリーズ　第6回　タンクモデル 【流出解析】シリーズ　第7回　積雪・融雪モデル　―降雪量・融雪量の推定― 【流出解析】シリーズ　第8回　タンクモデルの最適化 【流出解析】シリーズ　第9回　単位図法 【流出解析】シリーズ　第10回　流出量・流出高・比流量の違い 【流出解析】シリーズ　第11回　表面流モデル【定常降雨：前編】 【流出解析】シリーズ　第12回　表面流モデル【定常降雨：後編】

2．水文学におけるモデルとは

貯留関数法の説明に入る前に，流出モデルについて簡単に説明をしたいと思います．

【流出解析】シリーズの第1回でも取り上げたように水文学における流出解析という分野では，河川流量を推定することに重きが置かれています．

推定には一般に「流出モデル」が用いられます． 「流出モデル」は，「流出」と「モデル」という2つの言葉が組み合わさったものです． 「流出」とは，降った雨が地表や地中を流れて河川に入ることです．河川流量のことを流出量とも呼びます． また，水文学などの自然科学分野において「モデル」とは，現象を簡素化・抽象化したものです．

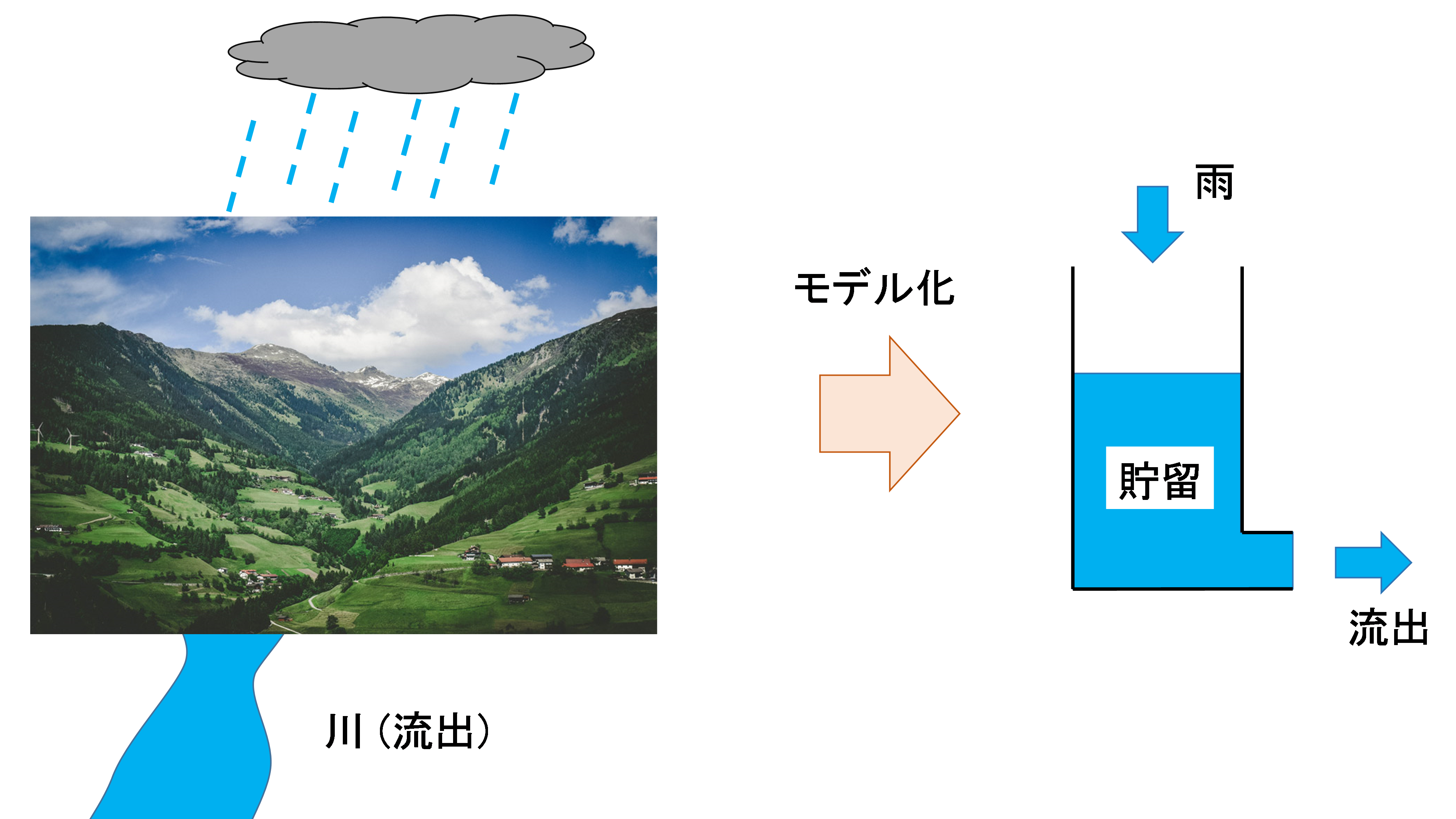
例えば，下図のように 陸地に降った雨が谷に集まり，川を形成して流れていくという過程は，タンク(陸地)に水(雨)が入り，タンクの穴(川)を通って排水(流出)されるというように単純化して捉えることができます． このように現象を単純化して捉えることが「モデル」の考え方です． 貯留関数法やタンクモデルのような流出モデルは，このように流域を1つのタンクとして捉え，流出過程を数式で表現しようという手法です．

まとめ：以下のように現象を抽象化(モデル化)しています．

現象・実際のもの	→	モデル
雨	→	タンクに入れる水
陸地	→	タンク
川	→	タンク底の穴
流出	→	排水

3．貯留関数法とは

3.1．貯留関数法の考え方

貯留関数法は，「流域を一つの貯水池とみたてて，流域貯留量と直接流出量(※)の関係から洪水流出現象を説明しようとする手法」で，主に短期流出(洪水流出)に使われています． ざっくり言えば，「流域内にいっぱい水が蓄えられているほど，流域から出てくる量(流出量)も多くなるだろうから，その関係を使って流出量を推定しよう」ということです．

※後ほど解説します．

具体的なイメージが沸かない人は，お風呂に貯めたお湯を抜くときの様子を観察してみてください． 浴槽の栓を抜いた直後は，浴槽内に水がいっぱいあるため水位はどんどん低下していきますが，水がかなり少なくなると水位は少しずつしか低下しないことが確認できると思います．

貯留関数法では，流域に降った雨が流域に貯留され，川を通って流域から出てくるという過程をタンクを使って表現しようとしています．

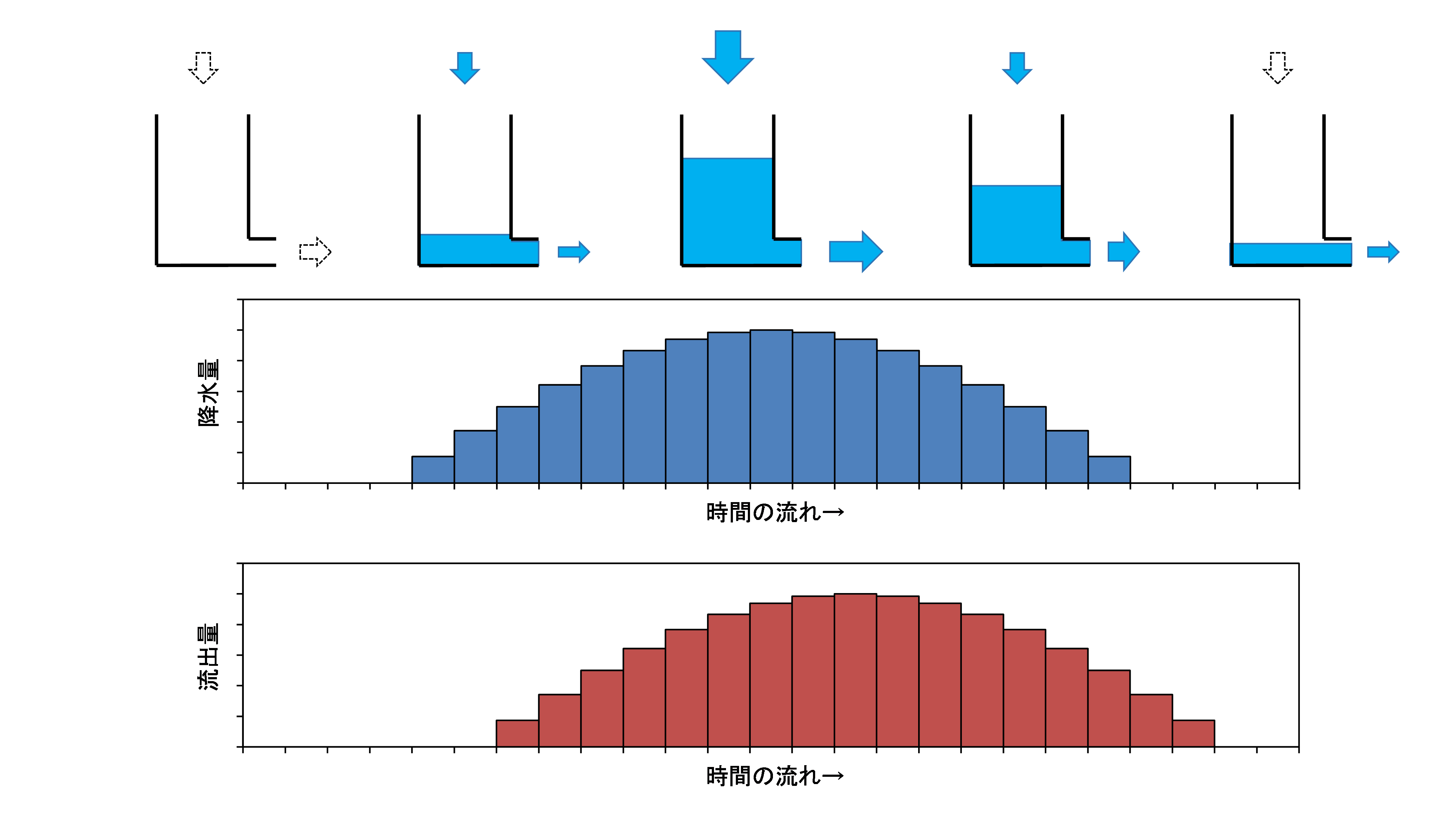
ところで，皆さんは降水量と流出量の時間的関係がどのようになっているか知っていますか？ 例えば，降った雨がすぐに排水される場合は，下図のようになります． 当然，降水量のピークと流出量のピークは一致します．

※実際には雨が降っていないときでも流域(タンク)内に水はありますが，ここでは雨によって流域(タンク)内に貯留される水のみを考えます．専門的には直接流出といいます．

しかし，現実には山に降った雨が一瞬で河口まで到達することはありません． これはなんとなく想像できると思います．

実際に，観測された降水量と流出量の間には，下図のように遅れが生じます．

貯留関数法とは，「流域を一つの貯水池とみたてて，流域貯留量と直接流出量の関係から洪水流出現象を説明しようとする手法」であると説明しました． 貯留関数法は，数学的に言えば，貯留量が流出量の一価関数であるという仮定の下に成り立っています． つまり，貯留量と流出量は1：1の関係にあり，流出量が決まれば，貯留量も一意に定まるというものです．

しかし，実際の貯留量と流出量の関係をみると，下図のようなループを描いてしまい，1：1の関係が成り立たなくなります．

そこで貯留関数法では，「ある時刻tに観測される流出量には降水量に対して時間的な遅れがあり，時刻tから遅れ時間TLだけ遡ったときの雨が流出したもの」と考えます． この遅れ時間の導入によりループが解消され，貯留量と流出量の間の1：1の関係が成立します． この「遅れ時間」の概念こそ，貯留関数法の特徴です．

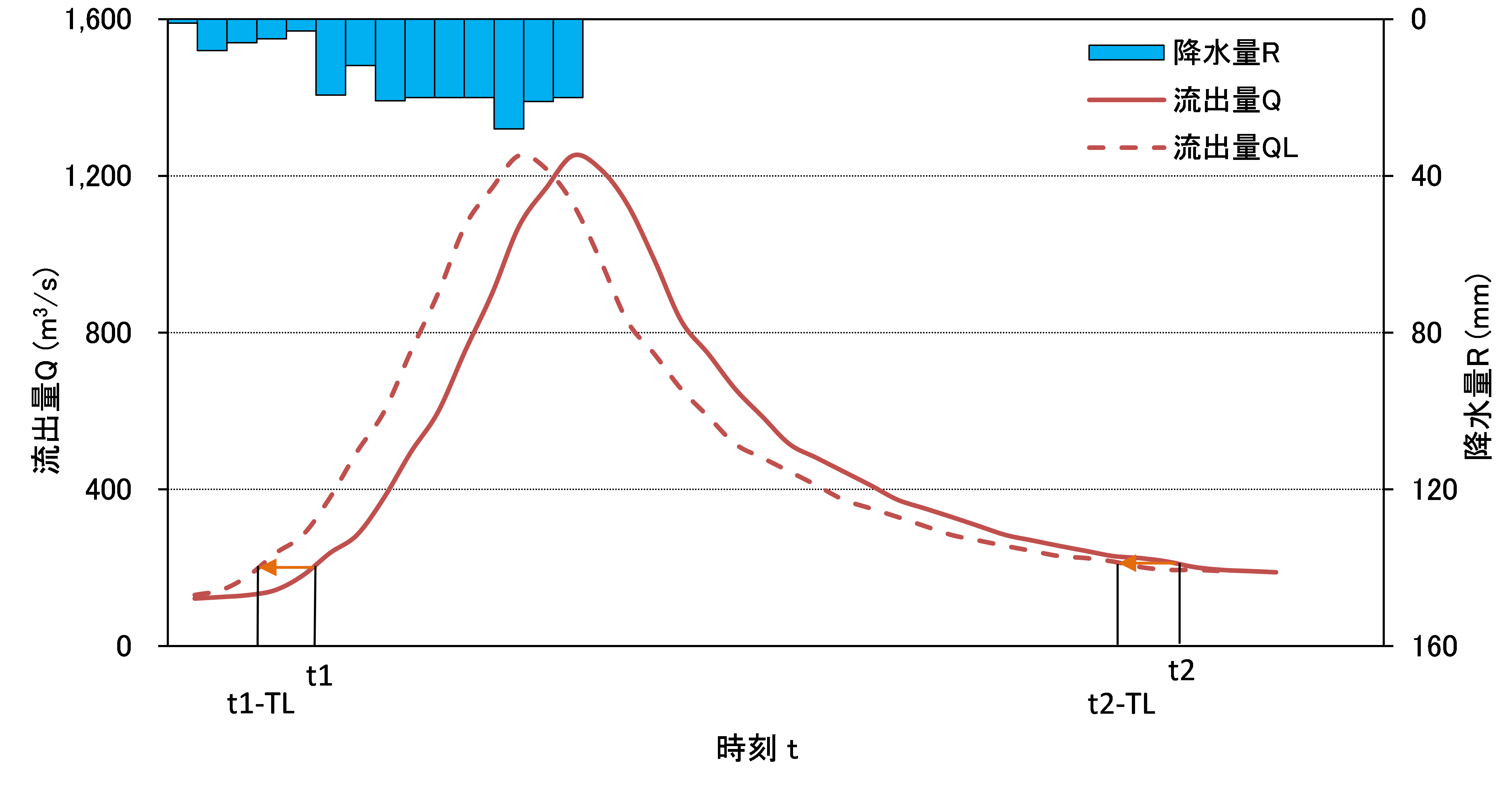
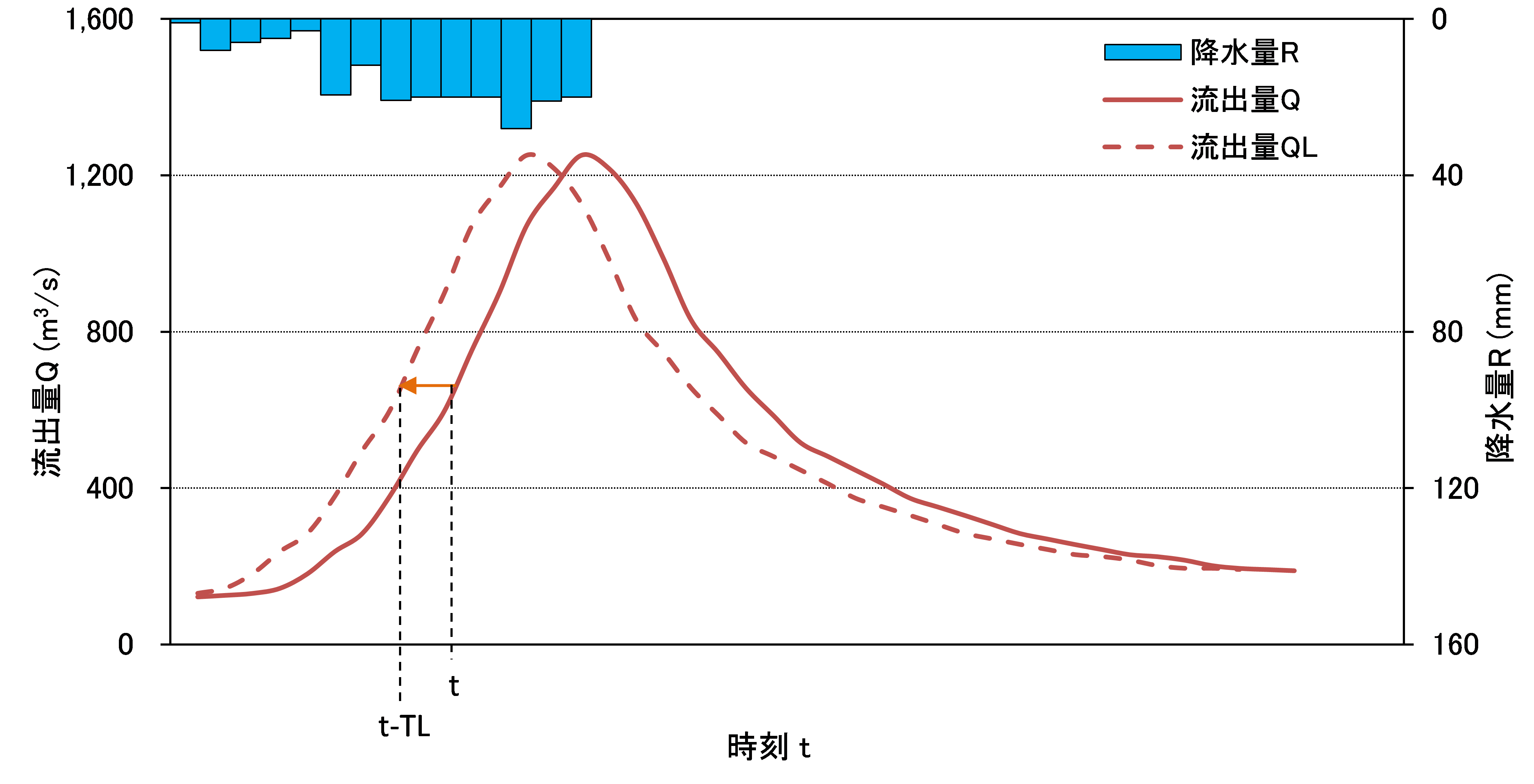
この考え方を図で表すと以下のようになります． 1．実際に観測された降水量\( R \)と流出量\( Q \)のグラフを描く． 2．遅れがないと仮定した場合には，降水量と流出量のピークは一致する．このときの流出量を\( Q_{L} \)で表す． 3．観測された流出量\( Q \)は，遅れがないときの流出量\( Q_{L} \)が遅れ時間\( T_{L} \)の分だけグラフの右方向(時間が進む方向)にシフトしたものと考える．また，時刻\( t \)の流出量\( Q(t) \)は時刻\( t-T_{L} \)の降水量\( R(t-T_{L}) \)に対応している．

なお，遅れ時間とは貯留量\( S \)のピークと流出量\( Q \)のピーク差であり，降水量のピークと流出量\( Q \)のピークの差ではないそうです．

3.2．貯留関数の基礎式

貯留関数法の考え方を数式で表すと以下のようになります．

\[ \begin{align} &\dfrac{dS}{dt} =\dfrac{1}{3.6}fAr-Q _{L}\\ &S = K {Q _{L}} ^{p}\\ &Q(t) =Q _{L}(t-T _{L})\\ \end{align} \]

ここで，

\[ \begin{align} 　　　　　S&：時刻tにおける流域貯留量 (m3/s・hr)\\ 　　　　　f&：ピーク流出係数 (-)\\ 　　　　　A&：流域面積 (km2)\\ 　　　　　r&：降雨強度 (mm/hr)\\ 　　　　　Q_{L}&：遅れ時間T_{L}がないと仮定したときの流出量 (m3/s)\\ 　　　　　Q&：観測された流出量 (m3/s)\\ 　　　　　T_{L}&：遅れ時間 (hr)\\ 　　　　　K，p&：パラメータ\\ \end{align} \]

1つ目の式は，水収支を表しており，貯留量の変化は入る量(降水)と出ていく量(流出)の差であることを表しています． 2つ目の式は，貯留量\( S \)と流出量\( Q_{L} \)が一価関数で表せると仮定したときの式です．つまり，貯留量がわかれば流出量も求まる．逆も然り． 3つ目の式は，遅れを表しており，ある時刻\( t \)の流出量\( Q \)が遅れ時間\( T_{L} \)だけ遡った流出量\( Q_{L}(t-T_{L}) \)に等しいことを表しています．

定数\( p \)は1/3〜1の範囲にありあます． 定数\( K \)は流域面積と土地利用状況によって異なります． 遅れ時間\( T_{L} \)は流域規模や出水規模に左右されます．

4．計算プロセス

貯留関数法を実際に計算するときに具体的にどう計算するかを説明します．

さて，地表に到達した降水は下図のような流出成分に分配されます． 今回の計算では短期流出を対象としているため，全流出量から基底流出量を差し引いた直接流出量を対象に計算をします．

4.1．使用データ

使用するデータは降水量と全流出量，流域面積，流路延長です． このデータを使って，流域の特性を示す\(K\)，\(p\)，\(T_{L}\)を求めます． ちなみに全流出量は河川流量と同義です． ワークシート名は「貯留関数法_較正」としてください．

流域面積	流域延長
600 km2	45 km

時刻t(h)	降水量R (mm)	全流出量Q (mm)	時刻t	降水量R (mm)	全流出量Q (mm)
1	1.0	122	21	0.0	656
2	8.0	126	22	0.0	586
3	6.0	131	23	0.0	516
4	5.0	144	24	0.0	481
5	3.0	181	25	0.0	446
6	19.4	238	26	0.0	411
7	11.8	284	27	0.0	374
8	20.8	379	28	0.0	352
9	20	496	29	0.0	330
10	20	598	30	0.0	307
11	20	753	31	0.0	284
12	28	900	32	0.0	270
13	21	1072	33	0.0	256
14	20	1169	34	0.0	243
15	0.0	1252	35	0.0	230
16	0.0	1218	36	0.0	225
17	0.0	1128	37	0.0	216
18	0.0	986	38	0.0	202
19	0.0	830	39	0.0	195
20	0.0	746	40	0.0	192
			41	0.0	189

エクセルに入力します． 流域面積(\( 600 km^{2} \))と流路延長(\( 45 km \))も入力しておいてください．

4.2．t1とt2の選定

はじめに，直接流出量を求めておきます． \(t=1\)のときは降水が全流出量には影響していないと考え，\( Q(1)=122 \)を基底流出として各時刻の全流出量\(Q(t)\)から引いて直接流出量\(Q_{d}(t)\)を求めます．

次に，ピーク流出係数\( f \)を求めるために，ハイドログラフ(流出量の折れ線グラフ)の増水側，減水側でだいたい同じ流出量になる時刻\( t_{1} \)と\( t_{2} \)を選びます．このときの増水側，減水側で同じ全流出量になる時刻の組み合わせはいくつかありますが，全流出量がピーク全流出量(\( Q(15)=1252 \))の1〜2割ぐらいのときの時刻とします．

※今回の\( t_{1} \)と\( t_{2} \)の選定はやや恣意的になっています．詳しくは後編で考察します．

「ハイドログラフの増水側，減水側で同じ流出高qcを与える時刻t1，t2を求める．qcはピーク流出高の1〜2割をとる．」 金丸昭治，高棹琢磨：朝倉土木工学講座4　水文学，朝倉書店，1975，p.206

なお，これ以降特に断りなく流出量という言葉が出てきたら，全て直接流出量であると考えてください．

4.3．木村の式によって遅れ時間TLの第一近似値を求める．

木村俊晃さんは，遅れ時間\( T_{L}(h) \)が流路延長\( L(km) \)の関数として表されるとして，次式を提案しました．

\[ \begin{align} T _{L} &= 0.0470L-0.56 (L>=11.9)\\ T _{L} &= 0 (L<11.9)\\ \end{align} \]

この木村の式で得られた遅れ時間\( T_{L-Kimura}\)を最適な遅れ時間\(OptT_{L}\)の第一近似値とします．

4.4．ピーク流出係数\(f\)の計算

式(3)において近似的に\(T_{L}=0\)とすると，

\[ Q(t) =Q _{L}(t) \]

\( t_{1} \)と\( t_{2} \)の定義より，

\[ Q _{L} (t _{1})=Q _{L} (t _{2}) \]

時刻\( t_{1} \)と\( t_{2} \)の貯留量をそれぞれ\( S_{1} \)と\( S_{2} \)とすると，

\[ S _{1}=KQ _{L} (t _{1}) ^ p=KQ _{L} (t _{2}) ^ p = S _{2} \]

となる． ここで式(1)について\( t_{1} \)から\( t_{2} \)まで積分すると，

\[ \begin{align} \dfrac{dS}{dt} &=\dfrac{1}{3.6}fAr(t)-Q _{L} (t)\\ dS &=\dfrac{1}{3.6}fAr(t)dt-Q _{L} (t)dt\\ \int _{S1}^{S2}dS &= \int _{t _{1}}^{t _{2}}\dfrac{1}{3.6}fAr(t)dt-\int _{t _{1}}^{t _{2}}Q _{L} (t)dt\\ S _{2}-S _{1} &= \dfrac{1}{3.6}fA\int _{t _{1}}^{t _{2}}r(t)dt-\int _{t _{1}}^{t _{2}}Q _{L} (t)dt\\ \dfrac{1}{3.6}fA\int _{t _{1}}^{t _{2}}r(t)dt&=\int _{t _{1}}^{t _{2}}Q _{L} (t)dt\\ f &=\dfrac{\int _{t _{1}}^{t _{2}}Q _{L} (t)dt}{\dfrac{1}{3.6}A\int _{t _{1}}^{t _{2}}r(t)dt}\\ f &= \dfrac{QT}{\dfrac{A}{3.6}RT} \end{align} \]

ただし，

\[ \begin{align} QT &=\int _{t _{1}}^{t _{2}}Q _{L} (t)dt\\ RT &=\int _{t _{1}}^{t _{2}}r(t)dt\\ \end{align} \]

このようにしてピーク流出係数を求めます．

4.5．貯留量Sの計算

4.4で得られたピーク流出係数\( f \)を使用して，式(1)から貯留量\( S \)と流出量\( Q_{L} \)の関係を求める．すなわち，時刻\( t \)における貯留量\( S(t) \)は次式で与えられる．

\[ \begin{align} S(t) &= \dfrac{A}{3.6} \int _{t _{1}}^{t}fr(t)dt -\int _{t _{1}}^{t}Q_{L}(t)dt\\ &= FI(t)-QS(t)\\ \end{align} \]

ただし，

\[ \begin{align} FI(t) &=\dfrac{A}{3.6} \int _{t _{1}}^{t}fr(t)dt\\ QS(t) &= \int _{t _{1}}^{t}Q_{L}(t)dt\\\ \end{align} \]

4.6．台形積分によるループ曲線の内部面積の計算と最適な遅れ時間OptTLの決定

最適な遅れ時間\( T_{L} \)がいくらかは，ループ曲線(\( S-Q_{L} \)曲線)の内部面積で評価します． \( t_{L}=0 \)から\( T_{L-Kimura}+1\)まで1時間刻みで遅れ時間を変化させ，内部面積をそれぞれ求めます． 内部面積が最小なとき，すなわちループが最も解消されるときが最適な遅れ時間\(OptT_{L}\)であるとします．

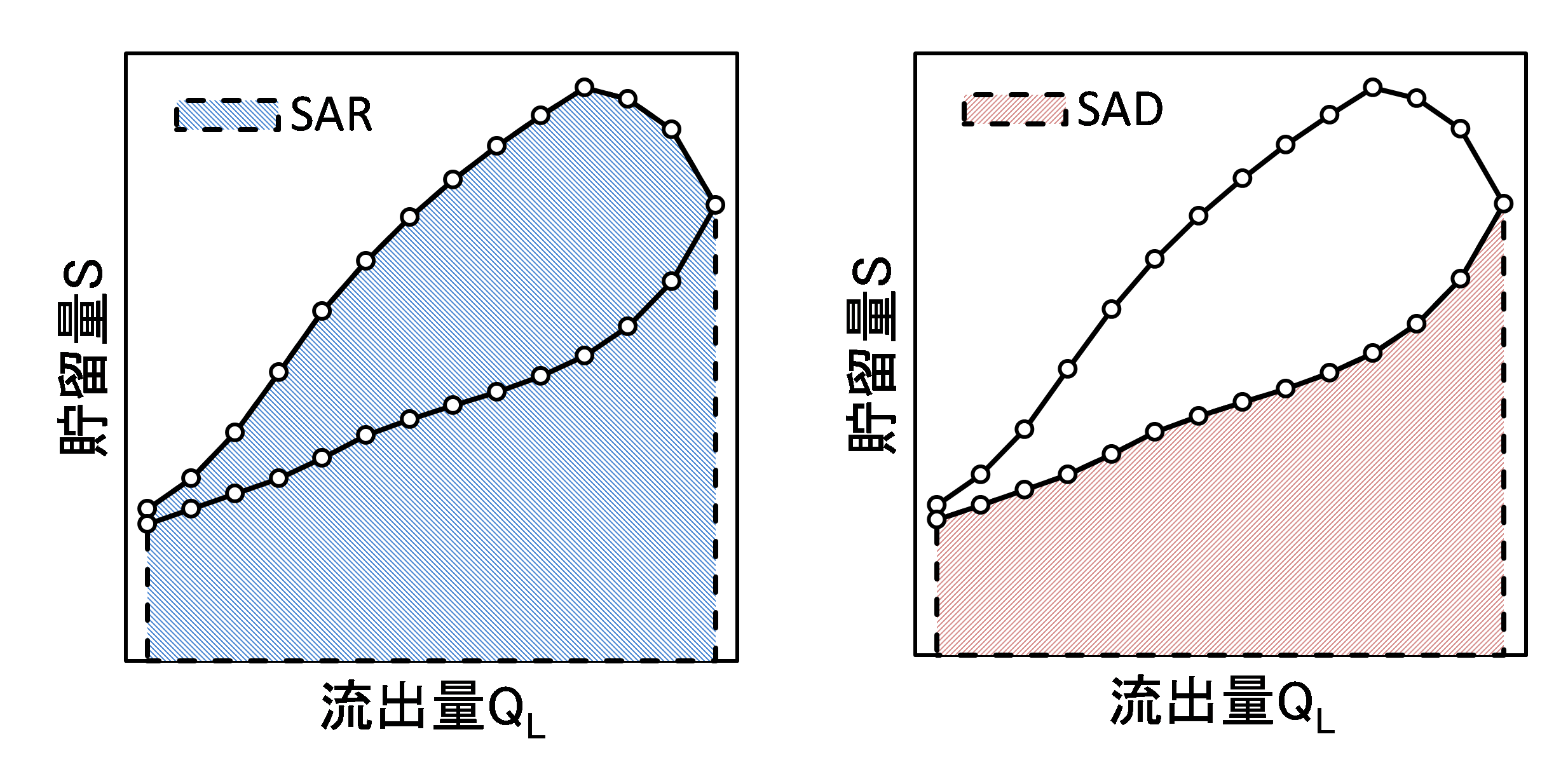
内部面積は台形積分によって求めます． プログラムでは，ループ曲線の上昇部分と\(Q_{L}\)軸で囲まれる面積をSAR，ループ曲線の下降部分と\(Q_{L}\)軸で囲まれる面積をSADとしています．

4.7．パラメータKとpの決定

最適な遅れ時間\(OptT_{L}\)が得られたら，最小二乗法によりパラメータ\( K \)，\( p \)を決定します． 式(2)より，

\[ \begin{align} S&= K {Q _{L}} ^{p} \\ \ln S &= \ln( K {Q _{L}} ^{p} )\\ &= \ln K + \ln{Q _{L}} ^{p}\\ &= \ln K + p\ln Q _{L}\\ \end{align} \]

ここで，

\[ \begin{align} Y&=\ln S\\ b&=\ln K \\ X&=\ln Q _{L}\\ \end{align} \]

とおくと，

\[ Y=pX+b \]

(\( X_{i} \),\( Y_{i} \))の\( E \)組のデータがあるとすると，最小二乗法より

\[ \begin{align} p&=\dfrac{\sum X_{i} \sum Y_{i}-E\sum X_{i} Y_{i}}{\sum X_{i} \sum X_{i} -E \sum {{X_{i}} ^{2}}}\\ K&=\exp \dfrac{\sum Y _{i}-p \sum X _{i}}{E}\\ \end{align} \]

高校数学の美しい物語：最小二乗法（直線）の簡単な説明

おわりに

最後までお付き合いいただき，ありがとうございました． 後編では，計算結果とプログラムを記載しているので，前編の内容と読み比べてみてください．

【流出解析】シリーズ　一覧

【流出解析】シリーズ　第1回　流域界の決定と入力データの用意 【流出解析】シリーズ　第2回　貯留関数法【前編】 【流出解析】シリーズ　第3回　貯留関数法【後編】 【流出解析】シリーズ　第4回　流域実蒸発散量の推定―蒸発散比法― 【流出解析】シリーズ　第5回　実蒸発散量の推定―補完法― 【流出解析】シリーズ　第6回　タンクモデル 【流出解析】シリーズ　第7回　積雪・融雪モデル　―降雪量・融雪量の推定― 【流出解析】シリーズ　第8回　タンクモデルの最適化 【流出解析】シリーズ　第9回　単位図法 【流出解析】シリーズ　第10回　流出量・流出高・比流量の違い 【流出解析】シリーズ　第11回　表面流モデル【定常降雨：前編】 【流出解析】シリーズ　第12回　表面流モデル【定常降雨：後編】

記事の内容に関してお気づきの点やご質問等がありましたら，ご連絡いただけますと幸いです． リクエスト等も受け付けておりますので，ご遠慮なく連絡ください． Twitterアカウント：エビぐんかん@6LxAi9GCOmRigUI メール：nnCreatorCircle@gmail.com

検索用キーワード：流出解析，流出モデル，水文学，洪水，治水，利水，数理モデル，貯留関数，表面流，タンクモデル，角屋睦，永井明博，

引用・参考文献

(1)河村三郎：土木工学プログラム集　水文・水理1　実用プログラムとグラフィック表示，森北出版株式会社，1984，pp.55-72 (2)丸山利輔，石川重雄，大槻恭一，高瀬恵次，永井明博，田中丸治哉，駒村正治，赤江剛夫，堀野治彦，三野徹，武田育郎，金木亮一，渡辺紹裕：地域環境水文学，朝倉書店，2014，pp.64-66 (3)角屋睦，永井明博，1980．講座　流出解析手法(その10) 4．貯留法―貯留関数法による洪水流出解析．農業土木学会誌48(10)，747-754． (4)藤村和正，井芹慶彦，鼎信次郎，岡田将治，村上雅博，2016．貯留関数式の最適パラメーターから評価する直接流出の分離について．第43回土木学会関東支部技術研究発表会．?-26．