1．はじめに

今回は、ベルヌーイの定理の応用例として大オリフィスを取り上げます。 ベルヌーイの定理については【水理学】ベルヌーイの定理とはを、小オリフィスについては【水理学】小オリフィス　―ベルヌーイの定理の応用―ご覧ください。

2．オリフィスとは？

オリフィスとは水面の側面や底面に開けられた孔のことです。ベルヌーイの定理を使うことでオリフィスからの水の流れを計算することができます。オリフィスには大オリフィスと小オリフィスがあります。縮流部（オリフィスから流れ出た水流が収縮する部分）での流速が一様とみなせるものを小オリフィスと呼びます。今回は、縮流部での流速が一様とみなせない大オリフィスを取り扱います。

3．大オリフィスの計算

ベルヌーイの定理は次式で表されます。

\[ \dfrac{v_{1} ^{2}}{2g} + z _{1} + \dfrac{p_{1}}{\rho g} =\dfrac{v_{2} ^{2}}{2g} + z _{2} + \dfrac{p_{2}}{\rho g} \]

ここで、 \(v _{1} \)、\(v _{2} \)：流速 \( (m/s) \) \(z _{1} \)、\(z _{2} \)：高さ\( (m) \) \(p _{1} \)、\(p _{2} \)：圧力 \( (Pa) \) \( g \)：重力加速度\( 9.8(m/s ^{2}) \) \( \rho \)：水の密度\( 1,000 (kg/m ^{3}) \)

大オリフィスの点1（水面）と点2（縮流部）にベルヌーイの定理を適用すると次式になります。

\[ \dfrac{v_{1} ^{2}}{2g} + H _{1} + \dfrac{p_{1}}{\rho g} = \dfrac{v_{z} ^{2}}{2g} + z ^{'} + \dfrac{p_{2}}{\rho g} \]

点1での圧力は静水圧分布とし、点2での圧力は大気圧として、\( p_{2} \)を0とすると

\[ \begin{align} \dfrac{v_{1} ^{2}}{2g} + (H _{1} - z ^{'}) + \dfrac{0}{\rho g} &=\dfrac{v_{z} ^{2}}{2g} + \dfrac{0}{\rho g} \\ \dfrac{v_{1} ^{2}}{2g} + z &= \dfrac{v_{z} ^{2}}{2g} \\ v _{z} = \sqrt{ 2g(h_{a} + z) } \end{align} \]

さらに接近流速による速度数等\( h_{a}\)を無視できる場合は次式になります。

\[ \begin{align} \dfrac{v_{1} ^{2}}{2g} + z &= \dfrac{v_{z} ^{2}}{2g} \\ 0 + z &= \dfrac{v_{z} ^{2}}{2g} \\ v_{z} &= \sqrt{2gz} \end{align} \]

例えば、水槽の容量が大きくてオリフィス（孔）が小さい場合には接近流速による速度水頭を無視することができます。

小オリフィスと同様にオリフィスからの流速と実際の流速には相違があります。これを補うために流速係数\( C_{v} \)を用いて実際の流速を表します。接近流速による速度水頭を無視できない場合は、\( V = C_{v} \sqrt{2g(h_{a}+z)} \)となります。無視できる場合は、\( V = C_{v} \sqrt{2gz} \)で表されます。

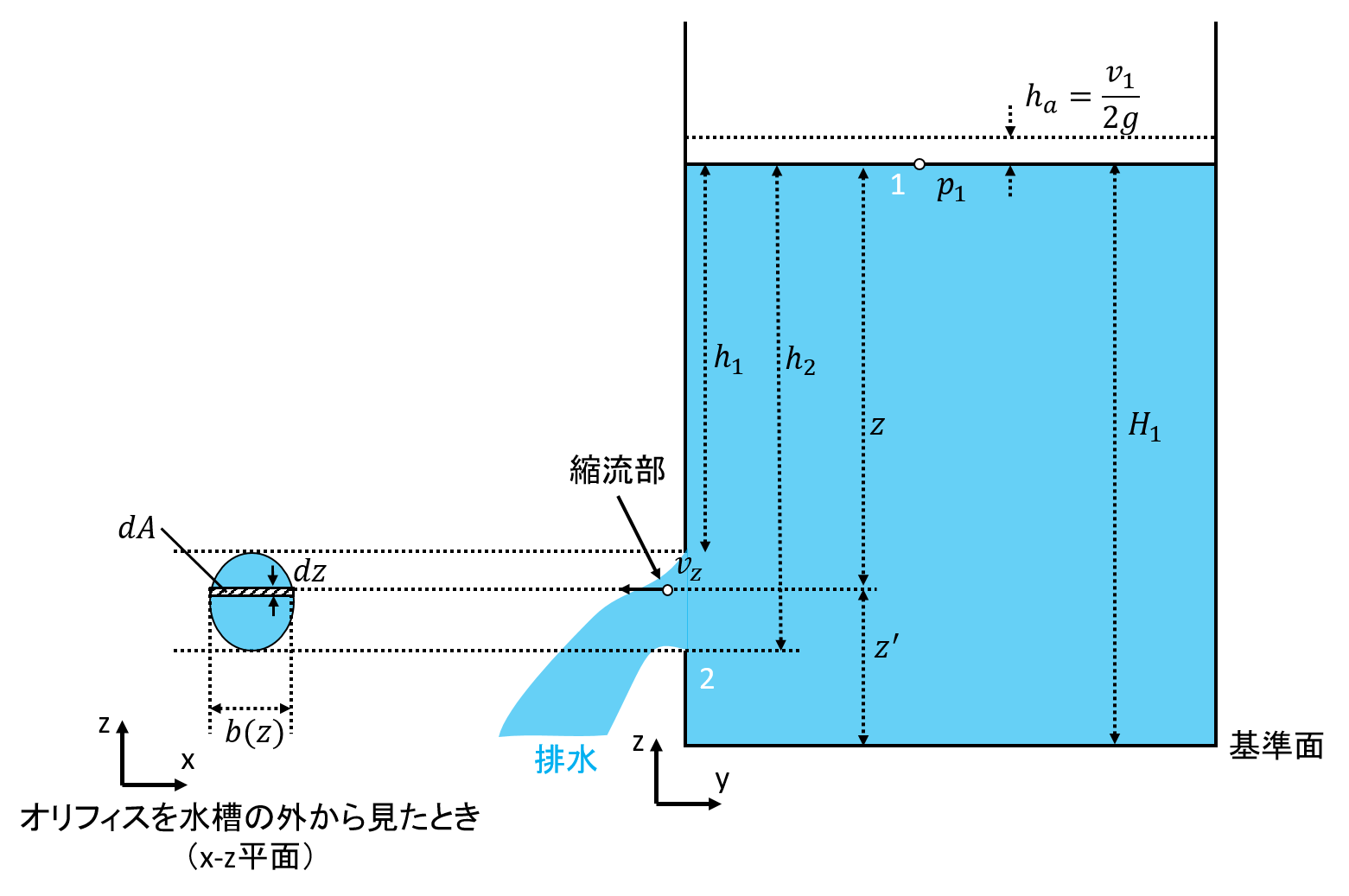
続いて、オリフィスからの流量\( Q \)を求めます。 まず、水槽の底から高さ\( z \)にある微小断面\( dA \)について考えます。 ここで、\( dA = b(z) \cdot dz\)とします。 流量は流速と断面積の積で表されますが、点2（縮流部）は収縮しているため、オリフィス（孔）の面積をそのまま流速にかけると誤差が生じます。そこで、小オリフィスと同様にオリフィス（孔）の面積に収縮係数\( C_{c} \)をかけて断面積は\( C_{c}dA \)となります。 したがって、接近流速による速度水頭を無視できない場合の微小断面\( C_{c}dA \)を通過する流量\( dQ \)は次式の通りになります。

\[ \begin{align} (流量) &= (流速) \times (断面積) \\ dQ &= C_{v} v_{z} \cdot C_{c} dA \\ &= C_{v} C_{c} \sqrt{ 2g(h_{a} + z) }\cdot b(z) \cdot dz \\ \end{align} \]

オリフィスからの流量\(Q \)は次式の通りです。

\[ \begin{align} Q &= \int _{h_{1}} ^{h _{2}}dQ \\ &= \int _{h_{1}} ^{h _{2}}C_{v} C_{c} \sqrt{ 2g(h_{a} + z) } b(z) dz \\ &= C_{v} C_{c}\sqrt{2g} \int _{h_{1}} ^{h _{2}} \left( h_{a}^{\tfrac{1}{2}}b(z) + z^{\tfrac{1}{2}} b(z) \right)dz \\ &= C_{v} C_{c}\sqrt{2g} \int _{h_{1}} ^{h _{2}} (h_{a} + z)^{\tfrac{1}{2}} b(z) dz \end{align} \]

実際のオリフィスはこのような形状ではなく長方形など単純な形をしていることが多いので、今回も長方形で考えてみます。

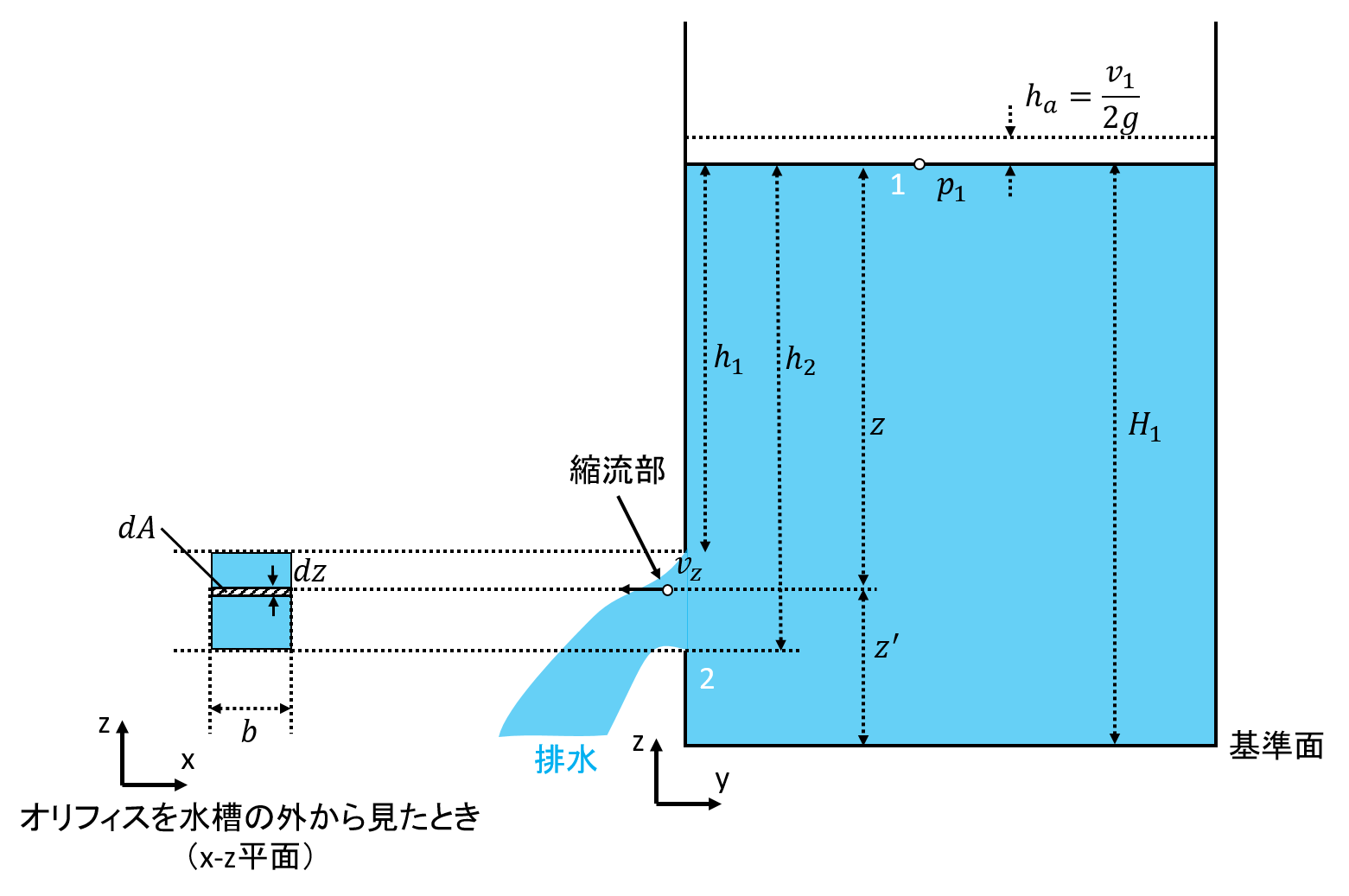
長方形のオリフィスの場合、幅\(b(z) \)は一定なので、オリフィスからの流量\(Q \)は次式の通りになります。

\[ \begin{align} Q &= C_{v} C_{c}\sqrt{2g} \int _{h_{1}} ^{h _{2}} (h_{a} + z)^{\tfrac{1}{2}} b dz \\ &= C_{v} C_{c}b\sqrt{2g} \int _{h_{1}} ^{h _{2}} (h_{a} + z)^{\tfrac{1}{2}} dz \\ &= \dfrac{2}{3}C_{v} C_{c}b\sqrt{2g} \left[ (h_{a} + z)^{\tfrac{3}{2}} \right] _{h_{1}} ^{h _{2}} \\ &= \dfrac{2}{3}C_{v} C_{c}b\sqrt{2g} \left( (h_{a} + h_{2})^{\tfrac{3}{2}} - (h_{a} + h_{1})^{\tfrac{3}{2}}\right) \end{align} \]

接近流速の速度水頭が無視できる場合は流量\(Q\)は次式で表されます。

\[ Q = \dfrac{2}{3}C_{v} C_{c}b\sqrt{2g} \left( h_{2}^{\tfrac{3}{2}} - h_{1}^{\tfrac{3}{2}}\right) \]

孔の大きさとオリフィスと水面の位置関係が分かれば流量が求められます。 式はの形は違えど、小オリフィスのように簡単な情報から流量が求められるのは面白いですね。

4．例題

簡単な例題ですが、大オリフィスの流量を計算してみましょう。 水面からオリフィス上端までの距離\( h_{1} \)を\( 1.9 m \)、水面からオリフィス下端までの距離\( h_{2} \)を\( 2 m \)、オリフィスの幅を\( 20 cm \)とします。 流速係数\( C_{v} \)を\( 0.98 \)、収縮係数\( C_{c} \)を\( 0.64 \)とします。 接近流速による速度水頭は無視できるものとします。

流量\(Q (cm ^{3}/s) \)は次の通りです。

\[ \begin{align} Q &= \dfrac{2}{3}C_{v} C_{c}b\sqrt{2g} \left( h_{2}^{\tfrac{3}{2}} - h_{1}^{\tfrac{3}{2}}\right) \\ &= 10 ^ {6} \cdot \dfrac{2}{3} \cdot 0.98 \cdot 0.64 \cdot \dfrac{20}{1000} \sqrt{2 \cdot 9.8} \left( 2^{\tfrac{3}{2}} - 1.9^{\tfrac{3}{2}}\right) \\ &\fallingdotseq 7755 \end{align} \]

5．おわりに

最後までお付き合い頂き、ありがとうございました。

今回の記事の内容はいかがだったでしょうか？ 本記事が水理学の勉強を支える一助になれば幸いです。

それでは、また次回の記事でお会いしましょう。

今後も農業農村工学(水文学、かんがい排水、土壌物理、水理学)を中に記事を執筆していきたいと思います。 リクエスト等も受け付けておりますので、ご遠慮なく連絡ください。 Twitterアカウント：エビぐんかん@6LxAi9GCOmRigUI メール：nnCreatorCircle@gmail.com

引用・参考文献

(1) 大津岩夫，安田陽一，高橋正行，高橋迪夫，長林久夫，藤田豊：水理学，理工図書株式会社，pp.84-86，2007． (2) 近畿高校土木会：解いてわかる！　水理，オーム社，pp.136-138，2012.