1．はじめに
今回は、水理学で一番重要で登場頻度も高い「ベルヌーイの定理」について解説したいと思います。ベルヌーイの定理の用途や導出過程について説明し、最後に簡単な例題を解いてみます。 本記事では、水理学を学び始めた方向けに、厳密さを欠いた説明があります。参考文献を併記しているので正確な話を知りたい人は参考文献をご覧ください。
2．ベルヌーイの定理
ベルヌーイの定理は次式で表されます。
ここで、 \(v _{1} \)、\(v _{2} \)：流速 \( (m/s) \) \(z _{1} \)、\(z _{2} \)：高さ\( (m) \) \(p _{1} \)、\(p _{2} \)：圧力 \( (Pa) \) \( g \)：重力加速度\( 9.8(m/s ^{2}) \) \( \rho \)：水の密度\( 1,000 (kg/m ^{3}) \)
ベルヌーイの定理をざっくり言うと、「川を流れる水やパイプの中を流れる水の任意の2点のエネルギーが等しい」という定理です。ベルヌーイの定理のおかげで水の流れを簡単に理解できるメリットがあります。 ちなみにベルヌーイの定理について厳密な話をすると、定常流、非圧縮性流れや粘性といったキーワードが出てきて話がややこしくなるので、ここでは割愛したいと思います。詳細に興味がある方は以下の参考書をご覧ください。
(1) 大津岩夫，安田陽一，高橋正行，高橋迪夫，長林久夫，藤田豊：水理学，理工図書株式会社，pp.31-33，2007．
下図は傾いたパイプの中を流れる水を表しています。
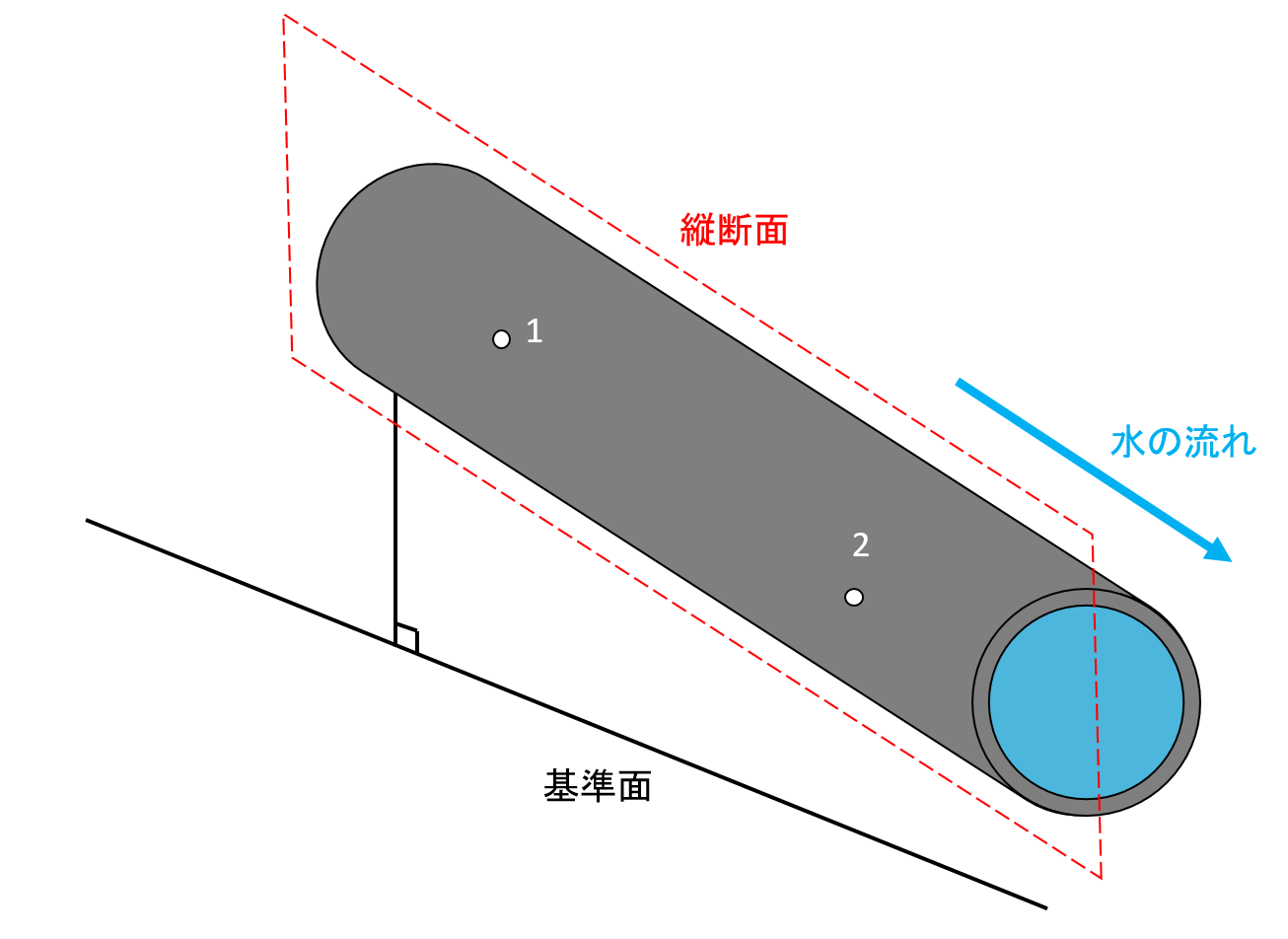このパイプを赤色の面（縦断面）で割って、左から見た図が下図になります。
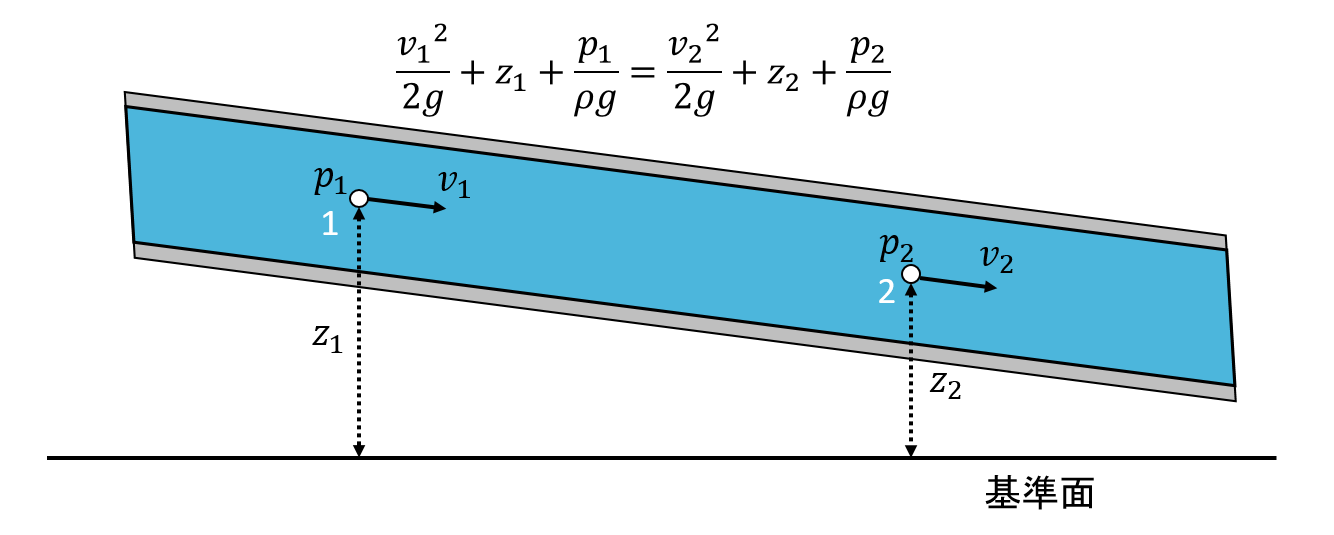
ここで点1の流速が\( v _{1} \)、基準面からの高さが\( z _{1} \)、圧力が\( p _{1} \)、点2の流速が\( v _{2} \)、基準面からの高さが\( z _{2} \)、圧力が\( p _{2} \)とします。このとき点1と点2の間には次式の関係が成り立ちます。
これがベルヌーイの定理です。次にベルヌーイの定理の各項について説明します。
左辺の第1項\( \tfrac{v_{1} ^{2}}{2g} \)は点1の運動エネルギーを長さの次元で表した「速度水頭」というものです。運動エネルギーが「速度水頭」に変換される理由をざっくり説明すると、ベルヌーイの定理を導出過程で式をわかりやすい形に整理していった結果この形になった、程度の理解で最初は問題ないです。同様に左辺の第2項\( z _{1} \)は点1の位置エネルギーを長さの次元で表した「位置水頭」、左辺の第3項\( \tfrac{p _{1}}{\rho g} \)は点1の圧力のなす仕事を長さの次元で表した「圧力水頭」です。同様に右辺は点2の速度水頭、位置水頭、圧力水頭を表しています。つまり、ベルヌーイの定理とは点1のエネルギーの和と点2のエネルギーの和が等しいということを表しています。
さて、このベルヌーイの定理の導出は実はとても簡単です。 ベルヌーイの定理の導出過程を知りたい方は下記参考書をご覧ください。
(1) 大津岩夫，安田陽一，高橋正行，高橋迪夫，長林久夫，藤田豊：水理学，理工図書株式会社，pp.31-33，2007．
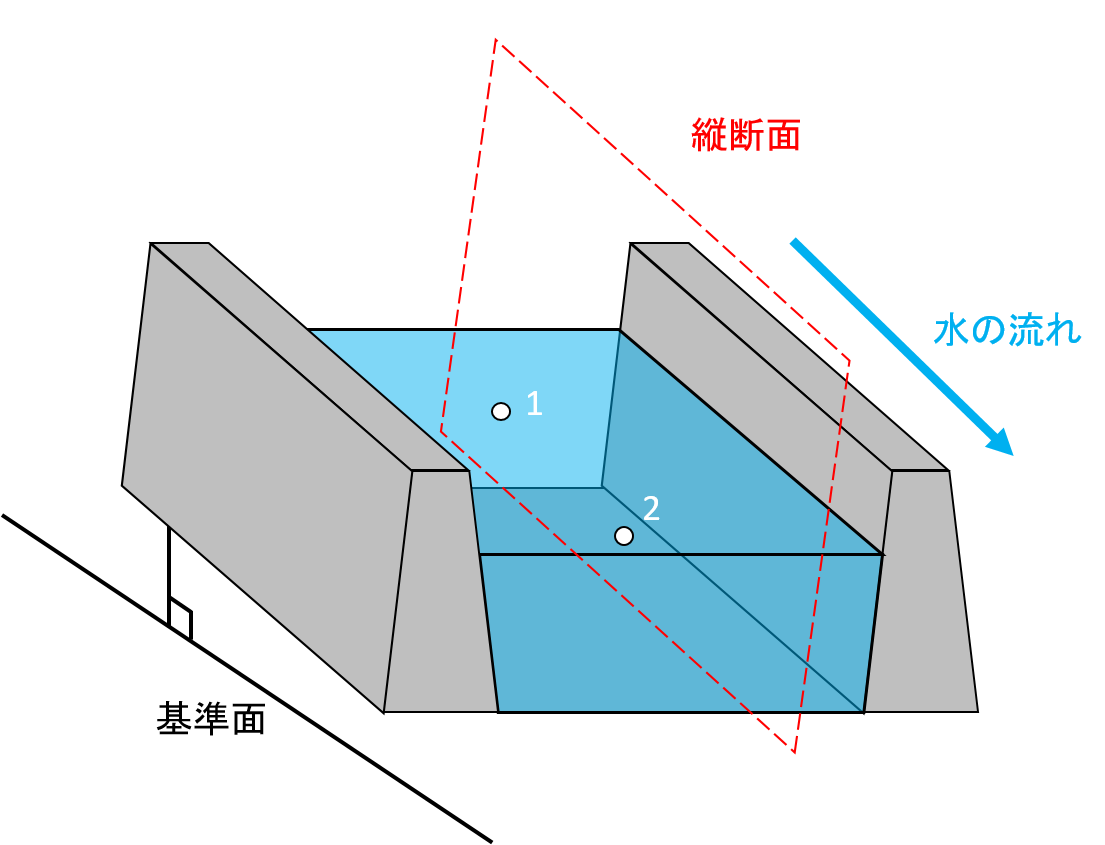
ちなみにベルヌーイの定理はパイプ（管水路）だけでなく、下図のような川の流れ（開水路）でも成立します。
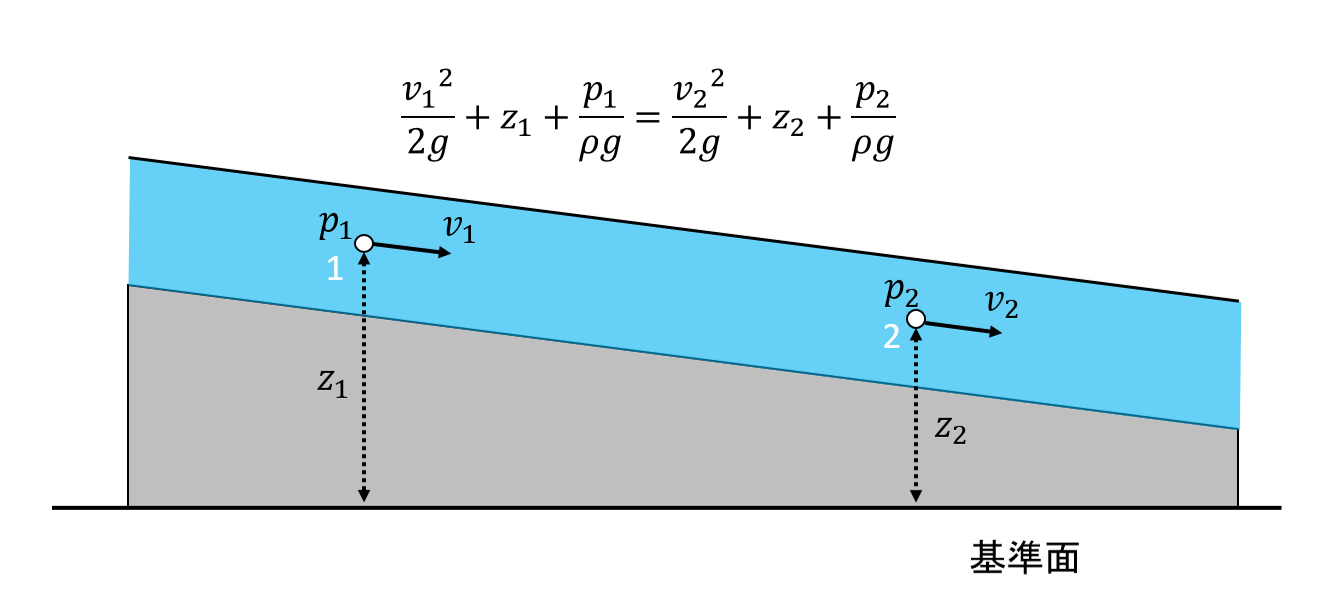
3．例題
簡単な例題ですが、ベルヌーイの定理を使ってみましょう。 点1の流速\( v _{1}\)が\( 5 (m/s) \)、高さ\( z _{1}\)が\( 10 (m) \)、圧力\( p _{1}\)が\( 200 (kPa) \)、点2の流速\( v _{2}\)が\( 6 (m/s) \)、高さ\( z _{2}\)が\( 8 (m) \)のとき、点2の圧力\( p _{2}\)を求めましょう。
よって、\( p _{2}\)は約\( 214 (kPa) \)です。
4．おわりに
最後までお付き合い頂き、ありがとうございました。
今回の記事の内容はいかがだったでしょうか？ 本記事が水理学の勉強を支える一助になれば幸いです。
それでは、また次回の記事でお会いしましょう。
今後も農業農村工学(水文学、かんがい排水、土壌物理、水理学)を中に記事を執筆していきたいと思います。 リクエスト等も受け付けておりますので、ご遠慮なく連絡ください。 Twitterアカウント：エビぐんかん@6LxAi9GCOmRigUI メール：nnCreatorCircle@gmail.com
引用・参考文献
(1) 大津岩夫，安田陽一，高橋正行，高橋迪夫，長林久夫，藤田豊：水理学，理工図書株式会社，pp.31-33，2007． (2) 近畿高校土木会：解いてわかる！ 水理，オーム社，pp.48-59，2012.
