1.岩井法による確率雨量の推定
確率雨量シリーズでは,これまで対数正規法および高瀬法(積率法)で確率雨量を求めました. 本記事では3つ目の岩井法を紹介したいと思います. ・対数正規法 ・高瀬法(積率法) ・岩井法 ・ガンベル・チャウの方法
第1回(対数正規法)および第2回(高瀬法(積率法))のページは以下になります.第1回(対数正規法)で確率雨量や計算方法について詳細に説明しているので,よかったらご覧ください.
【確率雨量】100年に1度の大雨ってどうやって計算しているの? ―第1回 対数正規法― 【確率雨量】100年に1度の大雨ってどうやって計算しているの? ―第2回 高瀬法(積率法)― 【確率雨量】100年に1度の大雨ってどうやって計算しているの? ―第3回 岩井法― 【確率雨量】100年に1度の大雨ってどうやって計算しているの? ―第4回 ガンベル・チャウの方法―
2.岩井法
農業農村工学(農業土木)や水文学に関わる学生にとって岩井法という言葉は一度は聞いたことがあるのではないでしょうか? というのも,日本における水利施設などの設計で確率雨量などを求めるときに使われる方法として最も一般的なものが岩井法だからです.
では,なぜ岩井法が最もポピュラーな方法なのか? 本記事の最後に岩井法の計算結果を踏まえて,その理由も考えてみたいと思います.
対数正規法と式の形は違えど,岩井法の考え方は対数正規法と大きく変わりません.
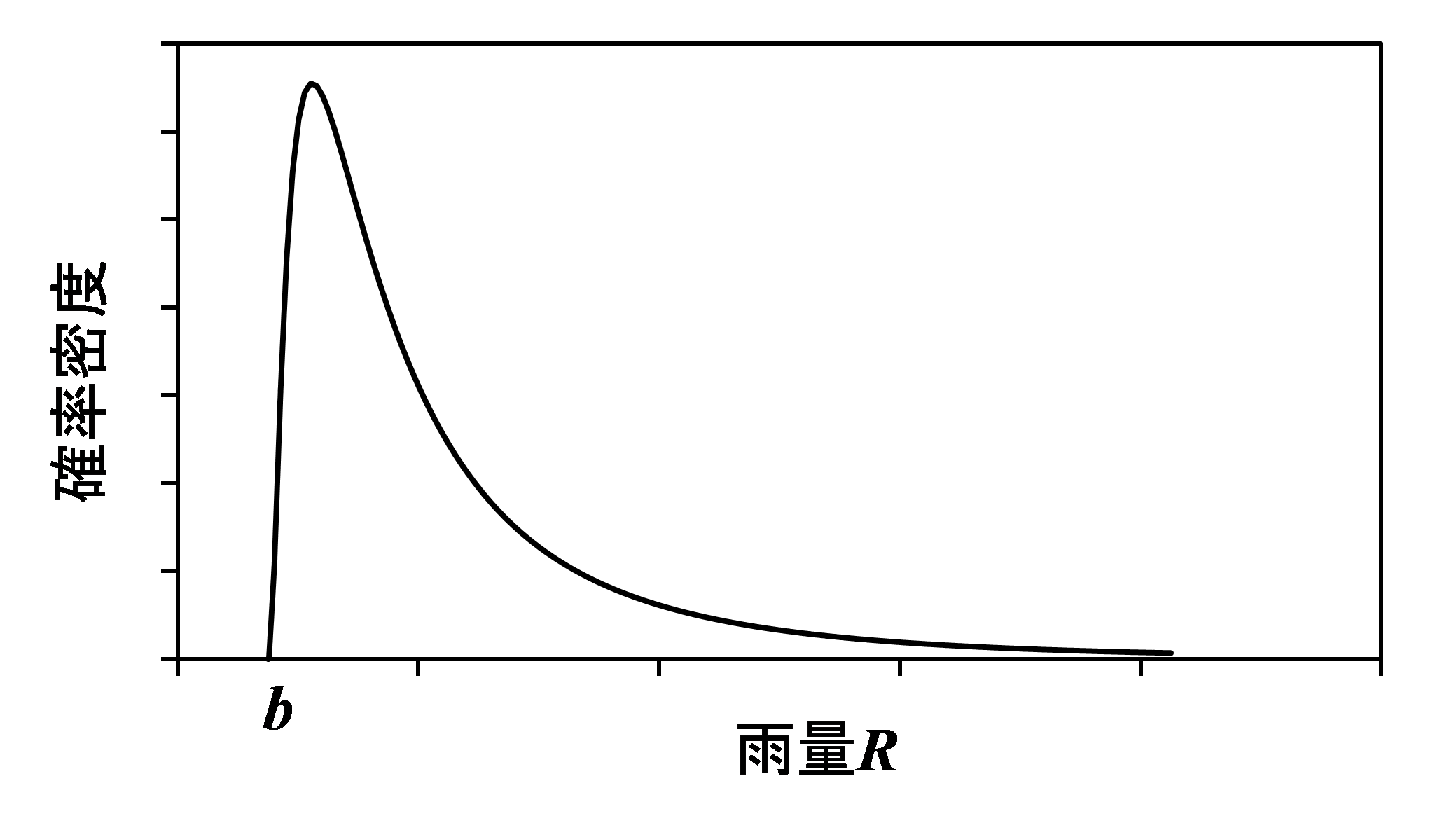
ただし,対数正規法では雨量の下限値を0としているのに対し,岩井法では雨量の下限値を\(b\)として与えています.
確かに,年最大日雨量や(降雨日の)日最大時間雨量が0になるよりは,なんらかの下限値\(b\)(>0)を持っているという方がリーズナブルな気がします.
岩井法の式
岩井法では,\( \xi \)は次式で表されます.
また,パラメータ\( a \),\( b \),\( R_{0} \)は次式で表されます. ただし,雨量データは降順(雨量\( R \)が大きい順)に並び替えられています.つまり,\( k=1 \)が最も雨量が多いデータを,\( k=N \)が最も雨量が少ないデータを指します.
なお,\(m\)は四捨五入して整数にします. また,\(N\)は雨量データの数です.
上記のパラメータ(\( \tfrac{1}{a} \),\(b\))が得られると,任意の超過確率に対する確率変数\(R\)は次式で与えられます.
3.計算用シートとプログラム
計算に用いたデータおよび計算結果をエクセルシートにまとめています.
入力データはエクセルのC列2行目〜21行目(雨量データ),H列2行目〜I列57行目(あらかじめ数値積分で求めたTとξ)です.
計算結果はエクセルのS列〜U列に出力されます.
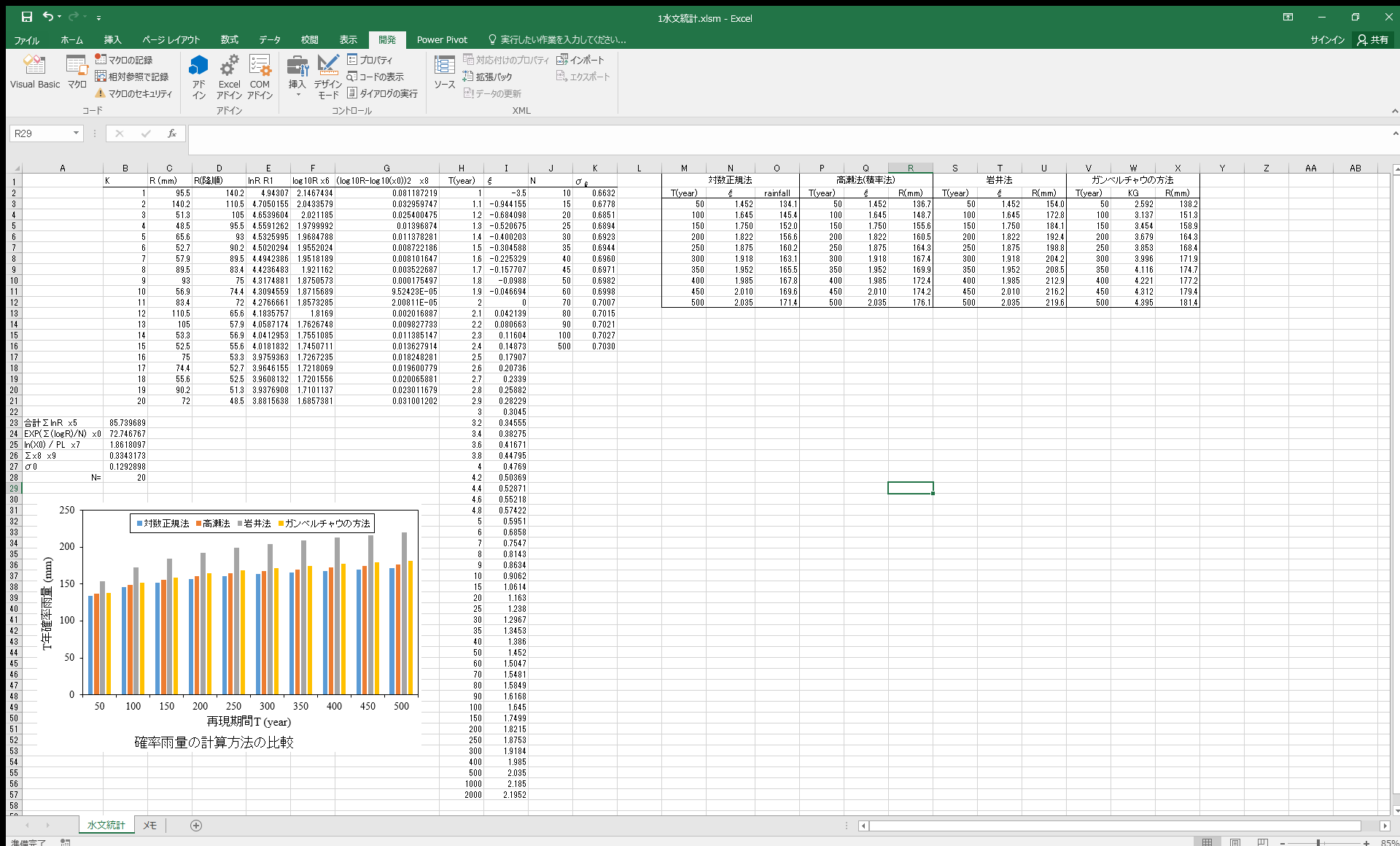
岩井法は,対数正規法や高瀬法(積率法)に比べて確率雨量を大きく見積もる性質があるようですね. 私見ではありますが,岩井法が日本で最もポピュラーな方法になったのはおそらくこれが理由ではないかと思います.
というのも,ある再現期間Tに対する確率雨量を大きく見るもるということは,より安全側(より大きな災害に耐えられるよう)に設計することになるからです. 第1回で紹介しましたが,水利施設(ダムや河川堤防など)はある確率雨量(例えば,100年に1回規模の降雨)に耐えられるように設計されます. つまり,同じ100年確率雨量に対して設計するとしても,その雨量が大きいほど施設はよい強い降雨災害に対応できるよう設計する必要があり,結果として安全になります(大きな雨に耐えられる). だから,確率雨量を大きく見積もる岩井法が採用されているのではないかと思います.
もちろん,より大きな水利施設を作ることはより多くの建設費用(税金)が必要ですが,水害が一度起きれば多くの人命が危険に晒されるため安全めに設計されているんでしょう.
実は「岩井法が確率雨量を大きく見積もる」から岩井法がポピュラーになったとかそんな高尚な理由ではないようです.なんとなく小難しくてそれっぽい式だからみたいな理由でメジャーになったようです. ちなみに,最近は単一のモデルで確率雨量を判断するのではなく,いくつかのモデルで計算して結果からはじき出されるある指標値を使って確率雨量を決定しているようです.詳しいことはまた別の記事で紹介したいと思います.
計算用エクセルファイルは下記URLからダウンロードできます.. ご自由にお使いください. 1水文統計.xlsm
Option Explicit
Function FNE(x As Double)
FNE = Exp(-x ^ 2)
End Function
Function swap(ByRef val1 As Double, ByRef val2 As Double)
'2津の変数を交換する関数
Dim temp As Double
temp = val1
val1 = val2
val2 = temp
End Function
Function BubbleSort(ByRef Array1() As Double, ByVal N As Integer, ByVal SortDirection As String)
'変数の定義
Dim cnt As Integer, i As Integer, j As Integer, k As Integer
'変数の初期化
cnt = 1
'エラー防止
If SortDirection <> "descending" And SortDirection <> "ascending" Then
MsgBox ("引数に誤りがあります.")
End
End If
Select Case SortDirection
'昇順並べ替え
Case Is = "ascending"
k = N - 1
Do While k >= 0
j = -1
i = 1
Do
If Array1(i) > Array1(i + 1) Then
j = i - 1
Call swap(Array1(i), Array1(i + 1))
End If
i = i + 1
Loop While i <= k
k = j
Loop
'降順並べ替え
Case Is = "descending"
k = N - 1
Do While k >= 0
j = -1
i = 1
Do
If Array1(i) < Array1(i + 1) Then
j = i - 1
Call swap(Array1(i), Array1(i + 1))
End If
i = i + 1
Loop While i <= k
k = j
Loop
End Select
End Function
Sub Iwai_Method()
'最終更新日:2020/7/19
'川村三郎:土木工学プログラム集 水文・水理1,森北出版,1984に準拠
'*********************プログラム起動時のメッセージを出力*********************
'Basicのプログラムの10〜430,1270〜1510は省略
Debug.Print "岩井法"
Debug.Print Format(Date) & " " & Hour(Time) & "時" & Minute(Time) & "分" & Second(Time) & "秒(S.K)"; " 計算開始"
Worksheets("水文統計").Activate
Application.ScreenUpdating = False
'*********************変数の定義*********************
'入力データや計算条件に関わる変数
Dim N As Integer 'データ数Number
Dim TS As Double '再現期間の初期値Time Start(年)
Dim TE As Double '再現期間の最終値Time End(年)
Dim SY As Double '再現期間のキザミStep Year(年)
Dim m As Integer 'ξデータの数
Dim slct As Integer '入力データの種類(雨量or流出量)の判別用
Dim R() As Double '降水量データを格納する配列
'普遍定数など
Dim p As Double '円周率
Dim PL As Double 'ln10
'集計用変数
Dim X5 As Double '自然対数をとったデータの合計値
Dim k As Integer, i As Integer, cnt As Integer
Dim X0 As Double 'EXP(自然対数をとったデータの平均値)
'シンプソン公式および試算法などに関わる変数
Dim E2 As Double 'ξ
Dim SG As Double '自然対数をとったデータの標準偏差
Dim A1 As Double '区間[A1,B1]に関して数値積分する
Dim C1 As Double '補正係数
Dim B1 As Double '区間[A1,B1]に関して数値積分する
Dim ND As Integer '積分範囲の分割数
Dim W As Double '超過確率
Dim W1 As Double '超過確率の第一次近似値
Dim E3 As Double 'ξの補正値(試算法で使用)
Dim x1 As Double 'シンプソン公式第二項
Dim x2 As Double 'シンプソン公式第三項
Dim S As Double '(π)^0.5/2/erf(ξ),シンプソン法を使用した数値積分で求める
Dim D As Double '数値積分における小区間の長さv
'確率雨量全般に関する変数
Dim x As Double '式(1.2.4)の左辺のx,つまり,T年確率降水量
Dim t As Double '再現期間
'岩井法に固有の変数
Dim small_m As Integer 'int(N/10)
Dim BK As Double '岩井法のパラメータbの途中式(1.4.4)のb(k)
Dim B2 As Double '岩井法のパラメータbの途中式(1.4.3)のΣb(k)
Dim b As Double '岩井法のパラメータb
Dim x6 As Double '岩井法のパラメータaの途中式(1.4.5)のlog10(R(k)+b)
Dim x7 As Double '岩井法のパラメータaの途中式(1.4.6)の(log10(R(k)+b))^2
Dim Y0 As Double '岩井法のパラメータaの途中式(1.4.5)のY0
Dim Y1 As Double '岩井法のパラメータaの途中式(1.4.6)のY1
Dim A As Double '岩井法のパラメータa
Dim K1 As Double 'ξ/a
Dim K2 As Double 'log10(x0+b)
Dim K3 As Double 'ξ/a+log10(x0+b)
Dim K4 As Double 'exp(ξ/a+log10(x0+b))
'*********************定数などの定義*********************
m = 56 'ξデータの数
X5 = 0 '自然対数をとったデータの合計値
p = 3.14159 '円周率
PL = 2.30259 'ln10(10の自然対数)
'*********************データ数および計算条件の入力*********************
N = InputBox("降雨または流量のデータ数を入力してください.")
TS = InputBox("再現期間の初期値(年)を入力してください.")
TE = InputBox("再現期間の最終値(年)を入力してください.")
SY = InputBox("再現期間のキザミ(年)を入力してください.")
'*********************入力データの種類(雨量or流出量)の入力と計算条件の出力*********************
Do
slct = InputBox("雨量なら1を,流出量なら2を入力してください.")
If slct = 1 Then
Debug.Print "R:降雨(mm)"
ElseIf slct = 2 Then
Debug.Print "R:流出量(m3/s)"
End If
Loop Until slct = 1 Or slct = 2
Debug.Print "再現期間の初期値(年)TS="; TS; "(year)"
Debug.Print "再現期間の最終値(年)TE="; TE; "(year)"
Debug.Print "再現期間のキザミ(年)SY="; SY; "(year)"
Debug.Print ""
Debug.Print "ORIGINAL DATA"
Debug.Print "データ数N="; N
'*********************入力データを降順に並び替える*********************
Cells(1, 4) = "R (mm) 降順"
ReDim R(1 To N)
'降水量データを取得
For i = 1 To N
R(i) = Cells(i + 1, 3)
Next i
'バブルソート
Call BubbleSort(R, N, "descending")
'降順に並び替えたデータをワークシートに表示
For i = 1 To N
Cells(i + 1, 4) = R(i)
Next i
'*********************入力データを計算用に加工する*********************
'BasicのプログラムのLOG(R),SUM(log(R)),exp(SUM/N) 430〜480の部分
'データの自然対数をとる
Cells(1, 5) = "lnR R1"
Cells(N + 3, 1) = "合計ΣlnR x5"
Cells(N + 3, 2) = 0
For k = 1 To N
Cells(k + 1, 5) = Log(Cells(k + 1, 4))
Cells(N + 3, 2) = Cells(N + 3, 2) + Cells(k + 1, 5)
Next k
X5 = Cells(N + 3, 2) '自然対数をとったデータの合計値
X0 = Exp(Cells(N + 3, 2) / N) 'EXP(自然対数をとったデータの平均値)
Cells(N + 4, 1) = "EXP(Σ(logR)/N) x0"
Cells(N + 4, 2) = X0
Debug.Print "x0="; X0
'*********************パラメータbの計算*********************
'COMP. OF b 510〜640
small_m = N / 10
For k = 1 To small_m
p = N + 1 - k
BK = (Cells(k + 1, 4) * Cells(p + 1, 4) - X0 ^ 2) / (2 * X0 - (Cells(k + 1, 4) + Cells(p + 1, 4)))
B2 = B2 + BK
Next k
b = B2 / small_m
Debug.Print "b="; b
'*********************パラメータaの計算*********************
'COMP. OF 1/a 1/aを求める 650〜750
For k = 1 To N
x6 = Log(Cells(k + 1, 4) + b) / PL
x7 = (Log(Cells(k + 1, 4) + b) / PL) ^ 2
Y0 = Y0 + x6
Y1 = Y1 + x7
Next k
Y0 = Y0 / N
Y1 = Y1 / N
A = Sqr(2 * N / (N - 1) * (Y1 - Y0 ^ 2))
Debug.Print "1/a="; A
'*********************計算結果用ラベル*********************
Cells(1, 19) = "岩井法"
Cells(2, 19) = "T(year)"
Cells(2, 20) = "ξ"
Cells(2, 21) = "R(mm)"
'*********************超過確率に対するξの値(E2),T年確率雨量xを計算する*********************
'COMP. OF KUSI線形補間法
'T>10では,線形補間法によってξを求める.再現期間Tに対する超過確率W1はシンプソン公式による数値積分から求める.
'T<=10では,線形補間法によってξの第1次近似値を与え,シンプソン公式により超過確率の第一近似値W1を得る.
'(続き)第一次近似値ξ,W1を使って,真の超過確率Wとの超過確率の近似値W1の差が十分に小さくなるまで試算法によって計算し,ξの値を決定する.
'(続き)T<=10では,xの変化量に対してerf(x)の変化量つまり,再現期間および超過確率が大きく変化するので試算法を用いる
cnt = 0
For t = TS To TE Step SY
'********************************************************************************************
'*********************T>10のとき,シンプソン法による数値積分でξを求める*********************
'********************************************************************************************
'*********************線形補間によりξの値(E2)を求める*********************
k = 0
Do
k = k + 1
Loop Until t < Cells(k + 2, 8)
k = k - 1
E2 = (Cells(k + 3, 9) - Cells(k + 2, 9)) / (Cells(k + 3, 8) - Cells(k + 2, 8)) _
* (t - Cells(k + 2, 8)) + Cells(k + 2, 9)
'予めTに対するξの値が得られているときは,数値積分と試算法はスルー
'TS,TE,SYを実数型で定義しているため「if t=Cells(k+2,8) then」だと正しく処理できない
If Abs(t - Cells(k + 2, 8)) < 0.0000001 Then
GoTo PerfectMatchingKusi
End If
'*********************数値積分*********************
A1 = 0 '区間[A1,B1]に関して数値積分する
C1 = 0.5 '補正係数
B1 = E2 '区間[A1,B1]に関して数値積分する
ND = 50 '積分範囲の分割数
W = 1 / t '超過確率
D = (B1 - A1) / (2 * ND) '区間[0, E2]をND個に分割(分母の2はシンプソン公式の第二項のxの値にするためのもの)
S = FNE(A1) + FNE(B1) 'シンプソン公式のf(a),f(b)に相当するFNE(A1),FNE(B1)をまずSに入れる
x1 = D 'シンプソン公式第二項
x2 = D + x1 'シンプソン公式第三項
For k = 1 To ND - 1
S = S + 4 * FNE(x1) + 2 * FNE(x2)
x1 = x2 + D
x2 = x1 + D
Next k
S = S + 4 * FNE(x1)
S = (S * D / 6) * 2 'erf(ξ)の積分範囲は[-ξ,ξ]だが,数値積分では[0,ξ]で積分しており,確率変数xはN(0,1)に従うので
W1 = 0.5 - S / Sqr(4 * Atn(1)) '式(1.2.8)
'*************************************************************************************************************************************
'*********************T<=10のときは,シンプソン公式による数値積分に加えて試算法も行うことで,最適なξの値を求める*********************
'*************************************************************************************************************************************
If t <= 10 Then
'真の超過確率Wとの超過確率の近似値W1の差が十分に小さくなるまで繰り返す
Do Until Abs(W - W1) <= 0.00005
'*********************補正係数の計算*********************
E3 = E2 - C1 * (W - W1) / W '第一次近似値から相対誤差の50%を引く
E3 = (E3 + E2) / 2
E2 = E3
B1 = E3
'*********************数値積分*********************
D = (B1 - A1) / (2 * ND) '区間[0, E2]を2*50に分割
S = FNE(A1) + FNE(B1) 'シンプソン公式のf(a),f(b)に相当するFNE(A1),FNE(B1)をまずSに入れる
x1 = D
x2 = D + x1
For k = 1 To ND - 1
S = S + 4 * FNE(x1) + 2 * FNE(x2)
x1 = x2 + D
x2 = x1 + D
Next k
S = S + 4 * FNE(x1)
S = (S * D / 6) * 2
'第二次近似値を求める
W1 = 0.5 - S / Sqr(4 * Atn(1))
Loop
End If
'**************************************************************************
'*********************T年確率雨量xを求める(結果の出力)*********************
'**************************************************************************
PerfectMatchingKusi:
Debug.Print "T="; t; "年確率雨量のξは"; E2
'確率変数x(確率雨量)の導出
K1 = A * E2
K2 = Log(X0 + b) / PL
K3 = K1 + K2
K4 = Exp(PL * K3)
x = K4 - b
Cells(3 + cnt, 19) = t
Cells(3 + cnt, 20) = E2
Cells(3 + cnt, 21) = x
cnt = cnt + 1
Next t
Debug.Print Format(Date) & " " & Hour(Time) & "時" & Minute(Time) & "分" & Second(Time) & "秒(S.K)"; " 計算終了"
Application.ScreenUpdating = True
End Sub
4.おわりに
防災や減災,人命救助などに関心のある人が農業農村工学に興味を持つきっかけとして本記事が貢献できれば幸いです. いよいよ次回は確率雨量シリーズの最終回,ガンベル・チャウの方法の記事になります. お楽しみに!
【確率雨量】100年に1度の大雨ってどうやって計算しているの? ―第1回 対数正規法― 【確率雨量】100年に1度の大雨ってどうやって計算しているの? ―第2回 高瀬法(積率法)― 【確率雨量】100年に1度の大雨ってどうやって計算しているの? ―第3回 岩井法― 【確率雨量】100年に1度の大雨ってどうやって計算しているの? ―第4回 ガンベル・チャウの方法―
本記事の執筆にあたり,書籍の内容について紹介することを快く承諾いただいた森北出版の皆様と,何より書籍の著者である河村三郎先生には心より感謝いたします.
確率雨量シリーズの第1回でも紹介しましたが,本記事の執筆にあたり,以下の書籍を参考にしました.この場を借りて厚く御礼申し上げます. 本記事で公開するプログラムは河村先生の書籍に書かれているもの(Basic)を元に,筆者がVBAで書いたものです. ミスには細心の注意を払っておりますが,完璧を保証するものではありませんので,以下の書籍をお手元にご用意いただくことをお勧めいたします.
河村三郎:土木工学プログラム集1 水文・水理1 実用プログラムとグラフィック表示,森北出版,1984 岩井重久,石黒政儀:応用水文統計学,森北出版,1970 石村園子:やさしく学べるラプラス変換・フーリエ解析 増補版,共立出版,2010
今後も農業農村工学(水文学,かんがい排水,土壌物理,水理学)を中心に記事を執筆していきたいと思います. リクエスト等も受け付けておりますので,ご遠慮なく連絡ください. Twitterアカウント:エビぐんかん@6LxAi9GCOmRigUI メール:nnCreatorCircle@gmail.com
検索用Key Words: 確率雨量,確率降水量,降雨,降水,水文事象,水文学,水文統計学,降雨事象,水利施設,設計,確率水文量,水文諸量,超過確率,非超過確率,リターンピリオド(return period),T年確率値,事象値,岩井法,ダム,河川堤防,防災,計算方法,解き方,プログラム,マクロ,やり方


