1．はじめに

今回の記事では円形断面水路と水理特性曲線について取り上げます。水理特性曲線は水路や水道管の設計において重要な概念ですが、何となく難しいイメージもあると思うので、その導出過程や役割についても触れながら解説したいと思います。

2．水理特性曲線とは

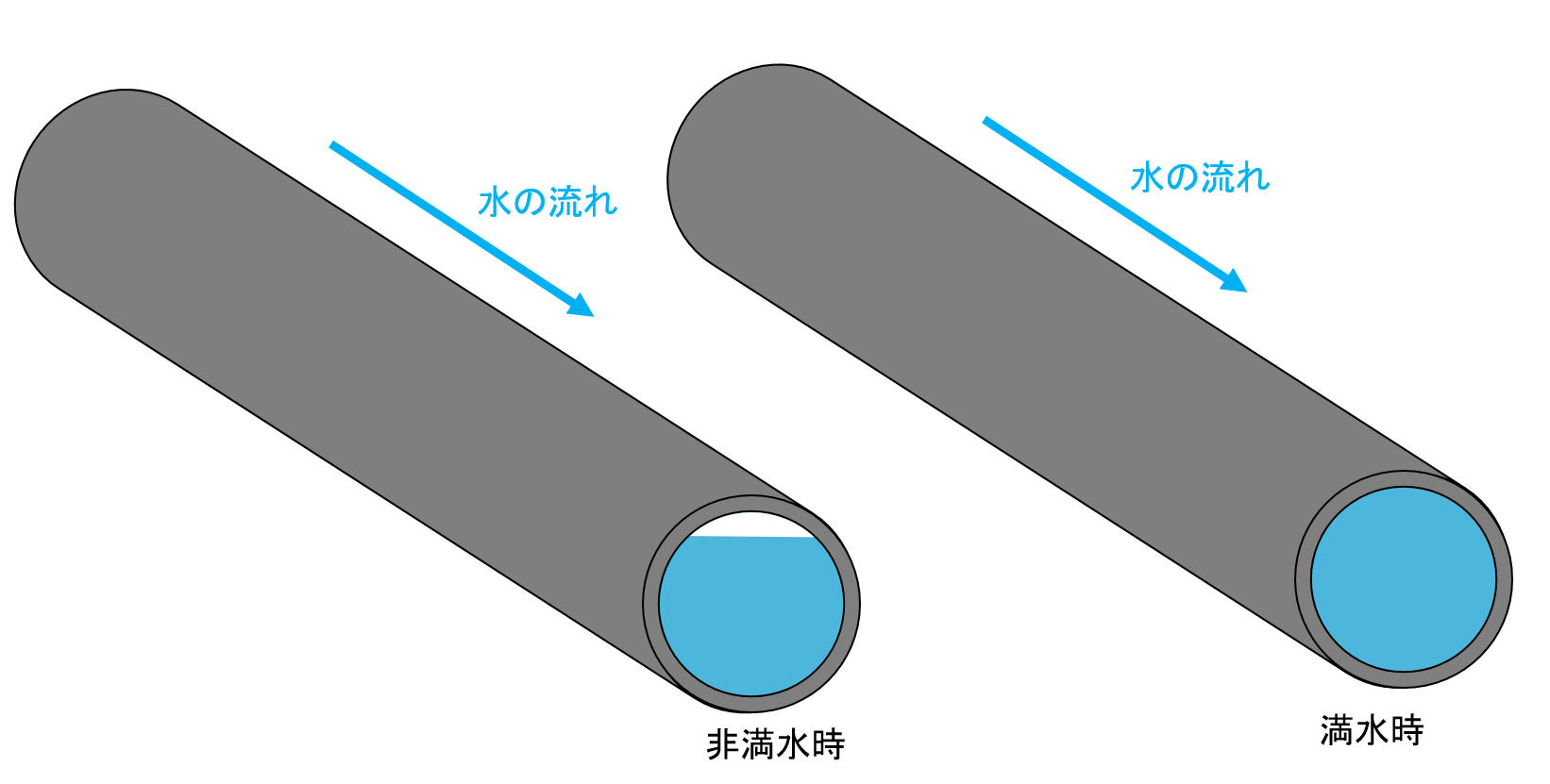その名の通り、円形断面水路とは横断面（水の流れる方向と垂直な平面で流路を切った断面）が円形である水路です。

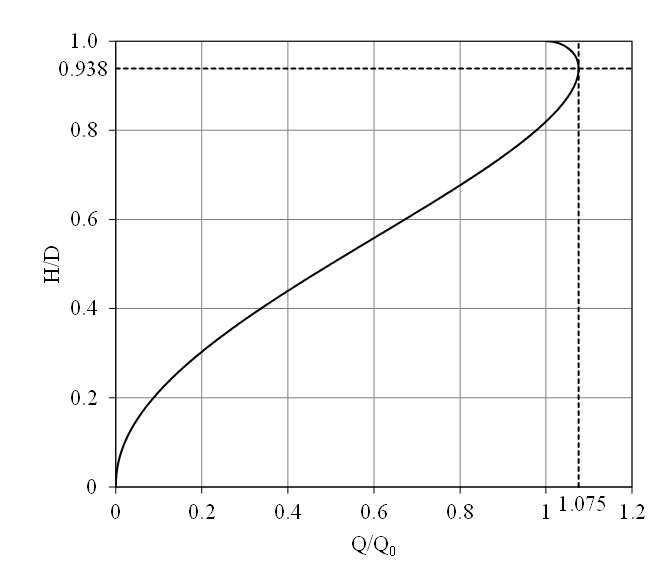　円形断面水路の水理特性曲線が上図です。水理特性曲線とは満水時の流量に対する流量の比\( \tfrac{Q}{Q _{0}}\)と満水時の水位に対する水位の比\( \tfrac{H}{D}\)をプロットしたものです。雨水管や地下河川として円形断面水路を設計する場合に、水路の寸法を決めたりするのに使われます。　水理特性曲線を見ると満水位\(D\)の93.8%にあたる水位で流量が最大になっています。このときの流量は満水状態で水を流した時(\( \tfrac{Q}{Q _{0}} = 1 \))よりも大きな値になっています。後ほど詳しく述べますが、実は円形断面水路では満水状態で水を流すよりも少し水位を下げて水を流した方が流量を増やすことができます。直感的には、水位が増えるほど流量は増えるように思えますが、実際には満水位付近では水位の増加によって流量が増えるのではなく、むしろ水路壁面との摩擦によって流量が減少します。水路を設計する際には設計目的に応じて流量が最大となるように水路の管の寸法を決定したり、流下速度が最大となるように寸法を決定したりします。このときに使われるものが水理特性曲線です。

3．円形断面水路の諸元

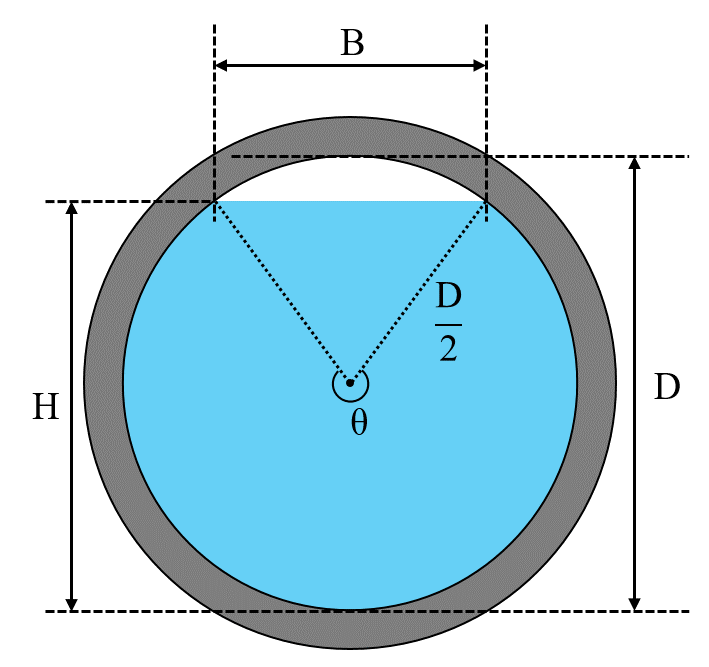円形断面水路の水理特性曲線を作るために必要な諸元を計算します。ここでは、満水時の水位\(D=0.9 (m)\)、水面勾配\(I=\tfrac{1}{1000} \)、粗度係数\(n=0.015\)とします。諸元の計算式は次の通りです。

\[ \begin{align} 水面幅& B =Dsin\dfrac{\theta}{2} \\ 潤辺& S=\dfrac{D}{2}\theta \\ 流積& A= \dfrac{D ^{2}}{8}(\theta -sin\theta) \\ 径深& R=\dfrac{A}{S} = \dfrac{D}{4} \left( 1 - \dfrac{sin \theta}{\theta} \right) \\ 水深& H = \dfrac{D}{2} \left( 1 - cos \dfrac{\theta}{2} \right) \\ 流速& v = \dfrac{1}{n} R^{\tfrac{2}{3}}I^{\tfrac{1}{2}} \\ 流量& Q = Av \end{align} \]

計算式の導出過程は本記事の最後に書いていますので、興味があればご覧ください。

4．円形断面水路と水理特性曲線

水を流していない状態は\(\theta = 0°\)、満水時は\(\theta = 360°\)になります。\(\theta \)を\(0° \)〜\(360° \)まで\(0.2° \)刻みくらいで変えながら流量\(Q \)を求めます。そして、流量\(Q\)を満水時の流量\(Q_{0}\)（\(\theta =360°\)の時の\(Q\)）で割ったものを横軸に、水位\(H\)を水位\(D\)で割ったものを縦軸にプロットすると水理特性曲線を描くことができます。円形断面水路の場合は満水位\(D\)の93.8%にあたる水位で流量が最大になります。これは満水位付近では水位の増加によって流量が増えるのではなく、むしろ水路壁面との摩擦によって流量が減少するため、このような曲線形状になります。

5．おわりに

最後までお付き合い頂き、ありがとうございました。

今回の記事の内容はいかがだったでしょうか？本記事が水理学の勉強を支える一助になれば幸いです。

それでは、また次回の記事でお会いしましょう。

今後も農業農村工学(水文学、かんがい排水、土壌物理、水理学)を中に記事を執筆していきたいと思います。リクエスト等も受け付けておりますので、ご遠慮なく連絡ください。 Twitterアカウント：エビぐんかん@6LxAi9GCOmRigUI メール：nnCreatorCircle@gmail.com

引用・参考文献

(1) 大津岩夫，安田陽一，高橋正行，高橋迪夫，長林久夫，藤田豊：水理学，理工図書株式会社，pp.107-109，2007． (2) 近畿高校土木会：解いてわかる！　水理，オーム社，pp.109-115，2012.

6．おまけ：各諸元の計算式の導出

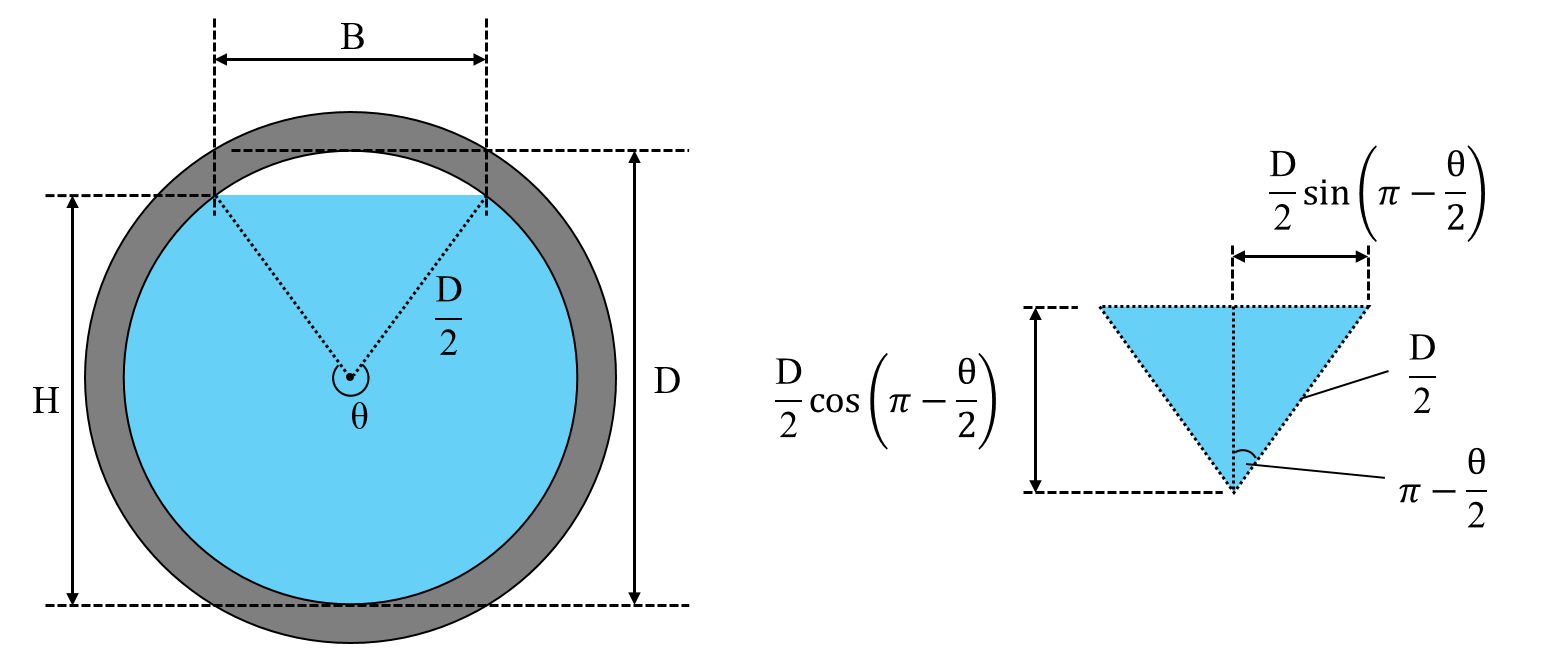
6.1．水面幅B

三角の部分に注目すると水面幅\(B\)を求めることができます。

\[ 水面幅 B =Dsin\dfrac{\theta}{2} \]

ここでは、水位が\(\tfrac{D}{2}\)以上の場合で説明していますが、水位が\(\tfrac{D}{2}\)未満の場合でも同じ考え方で水面幅\(B\)を求めることができます。

6.2．潤辺S

潤辺\(S\)は円弧の長さを求める式をそのまま使用して求めることができます。

\[ 潤辺 S=\dfrac{D}{2}\theta \]

LANCEMORE No.003 扇形の面積と円弧の長さ

6.3．流積A

潤辺\(A\)は扇の面積と三角形部分の面積を求める式を使用して求めることができます。

\[ \begin{align} 流積 A &= \dfrac{1}{2} \cdot \dfrac{D}{2} \cdot \dfrac{D}{2}\theta + \dfrac{1}{2} \cdot Dsin \left( \pi - \dfrac{\theta}{2} \right) \cdot \dfrac{D}{2}cos \left( \pi - \dfrac{\theta}{2} \right) \\ &= \dfrac{D ^{2}}{8} \theta + \dfrac{2 D^{2}}{8} sin \left( \pi - \dfrac{\theta}{2} \right) cos \left( \pi - \dfrac{\theta}{2} \right) \\ &= \dfrac{D ^{2}}{8} \theta - \dfrac{2 D^{2}}{8} sin \dfrac{\theta}{2} cos \dfrac{\theta}{2} \\ &= \dfrac{D ^{2}}{8} \theta - \dfrac{2 D^{2}}{8} \cdot \dfrac{1}{2} \left( sin \theta -sin 0 \right) \\ &= \dfrac{D ^{2}}{8}(\theta -sin\theta) \\ \end{align} \]

水面幅\(B\)を求めたときと同様に、水位が\(\tfrac{D}{2}\)以上の場合で説明していますが、水位が\(\tfrac{D}{2}\)未満の場合でも同じ考え方で水面幅\(B\)を求めることができます。

6.4．径深R

径深\( R \)はその定義より流積\( A \)を潤辺\( S \)で割って求めることができます。

6.5．水深H

水深\( H \)も流積Aと同じように三角形部分と分けて考えます。

\[ \begin{align} 水深H & = \dfrac{D}{2} + \dfrac{D}{2}cos \left( \pi - \dfrac{\theta}{2} \right)\\ & = \dfrac{D}{2} - \dfrac{D}{2}cos \dfrac{\theta}{2}\\ & = \dfrac{D}{2} \left( 1 - cos \dfrac{\theta}{2} \right) \\ \end{align} \]